[重返NOIP]动态规划1——NOIP2002普及组过河卒

题目描述

棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，$A$ 点 $(0, 0)$、$B$ 点 $(n, m)$，同样马的位置坐标是需要给出的。

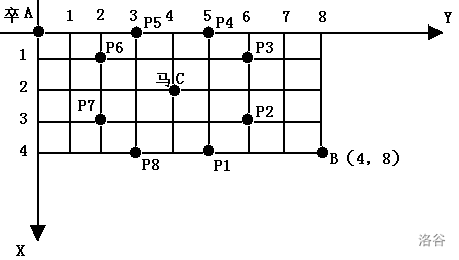
现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

样例 #1

样例输入 #1

6 6 3 3

样例输出 #1

提示

对于 $100 \%$ 的数据，$1 \le n, m \le 20$，$0 \le$ 马的坐标 $\le 20$。

【题目来源】

NOIP 2002 普及组第四题

思路

很简答，结合递归的想法，先把所有格子赋值为0，被马挡的格子标为2，只要碰到就return相应值就行

代码

#include<stdio.h>
int bx,by,mx,my;
int f(int **pan1,int bx1,int by1,int zx1,int zy1){
    if(zy1+1<=by1&&zx1+1<=bx1){
        if(pan1[zy1+1][zx1]==0||pan1[zy1][zx1+1]==0) return f(pan1,bx1,by1,zx1+1,zy1)+f(pan1,bx1,by1,zx1,zy1+1);
        else return 0;
    }else if(zy1==by1&&zx1+1<=bx1){
        return f(pan1,bx1,by1,zx1,zy1+1);
    }else if(zy1+1<=by1&&zx1==bx1){
        return f(pan1,bx1,by1,zx1+1,zy1);
    }else if(zy1==by1&&zx1==bx1){
        return 1;
    }else return 0;
}
int main(){
    scanf("%d %d %d %d",bx,by,mx,my);
    int zx=0,zy=0,pan[by+1][bx+1];
    for(int i=0;i<=by;i++){
        for(int j=0;j<=bx;j++){
            pan[i][j]=0;
        }
    }
    pan[my][mx]=1;
    if(mx+1<=bx&&my+2<=my) pan[my+2][mx+1]=1;
    if(mx-1<=bx&&my+2<=my) pan[my+2][mx-1]=1;
    if(mx-2<=bx&&my+1<=my) pan[my+1][mx-2]=1;
    if(mx+2<=bx&&my+1<=my) pan[my+1][mx+2]=1;
    if(mx+1<=bx&&my-2<=my) pan[my-2][mx+1]=1;
    if(mx-1<=bx&&my-2<=my) pan[my-2][mx-1]=1;
    if(mx-2<=bx&&my-1<=my) pan[my-1][mx-2]=1;
    if(mx+2<=bx&&my-1<=my) pan[my-1][mx+2]=1;
    printf("%d",f(pan,bx,by,zx,zy));
}

（由于尚未搞清的原因，上述代码还无法运行，具体错误也还没发现）

高级的思路

这道题初始位置是从 0 开始的，这样不是很利于我们解题，所以不如暂且把这题里涉及的坐标统统 +1，那么初始位置就从（0,0）（0,0）变成了（1,1）（1,1）。

先考虑如果没有任何马的限制，卒子可以随便向右向下走，那么可以想到，一个卒子只能从当前格子的左侧格子和当前格子的上方格子上走到当前格子。那么假设从（1,1）（1,1）走到当前格子的左侧格子的路径条数是 xx，从（1,1）（1,1）走到当前格子的上方格子的路径条数是 yy，那么从（1,1）（1,1）走到当前格子的路径条数就应该是 x+yx+y。

其实我们已经得到了一个动态规划的转移方程，设 f（i,j）f（i,j）表示从（1,1）（1,1）格子走到当前格子的路径条数，那么根据上一段得到的结论，可以得到：

f（i,j） = f（i-1,j） + f（i,j-1）
f（i,j）=f（i−1,j）+f（i,j−1）

（i,j）（i,j）是当前格子，那么（i-1,j）（i−1,j）就是当前格子的上方格子，（i,j-1）（i,j−1）就是当前格子的左侧格子。我们只需要从小到大依次枚举 ii 和 jj 就能获得所有点的答案，可以想到，在这道题里我们要求的答案就是 f（n,m）f（n,m）（因为 B 点的坐标是（n,m）（n,m））。

当然如果只是按照这个公式推肯定不行，因为 ff 的初始数值都是 0，再怎么推也都是 0，我们要让 f（1,1）f（1,1）能根据上面得到的式子推出答案是 1，这样才能有有意义的结果。根据 f（1,1）=f（0,1）+f（1,0）f（1,1）=f（0,1）+f（1,0），我们只需要让 f（1,0）=1f（1,0）=1 或者 f（0,1）=1f（0,1）=1 即可。

接下来考虑一下加入了马这道题该怎么做，假设（x,y）（x,y）这个点被马拦住了，其实就是说这个点不能被卒子走到，那当我们枚举到这个点的时候，发现他被马拦住了，那就直接跳过这个点，让 f（x,y）=0f（x,y）=0 就行了。

具体写代码的时候我们注意到在判断一个点有没有被马拦住时，会用到（i-2,j-1）（i−2,j−1）和（i-1,j-2）（i−1,j−2）这两个位置，那如果不把所有的点的坐标都加上 2 （前面分析的时候只把所有的坐标加上 1），就会因为数组越界而 WA 掉一个点。

答案可能很大，所以记得开 long long

高级的代码

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;

const int fx[] = {0, -2, -1, 1, 2, 2, 1, -1, -2};
const int fy[] = {0, 1, 2, 2, 1, -1, -2, -2, -1};
//马可以走到的位置

int bx, by, mx, my;
ll f[40][40];
bool s[40][40]; //判断这个点有没有马拦住
int main(){
    scanf("%d%d%d%d", &bx, &by, &mx, &my);
    bx += 2; by += 2; mx += 2; my += 2;
    //坐标+2以防越界
    f[2][1] = 1;//初始化
    s[mx][my] = 1;//标记马的位置
    for(int i = 1; i <= 8; i++) s[mx + fx[i]][my + fy[i]] = 1;
    for(int i = 2; i <= bx; i++){
        for(int j = 2; j <= by; j++){
            if(s[i][j]) continue; // 如果被马拦住就直接跳过
            f[i][j] = f[i - 1][j] + f[i][j - 1];
            //状态转移方程
        }
    }
    printf("%lld\n", f[bx][by]);
    return 0;
}

题目描述#

输入格式#

输出格式#

样例 #1#

样例输入 #1#

样例输出 #1#

提示#

思路#

代码#

高级的思路#

高级的代码#