题目描述
在高为 $H$ 的天花板上有 $n$ 个小球,体积不计,位置分别为 $0,1,2,\cdots,n-1$。在地面上有一个小车(长为 $L$,高为 $K$,距原点距离为 $S_1$)。已知小球下落距离计算公式为 $d=0.5 \times g \times (t^2)$,其中 $g=10$,$t$ 为下落时间。地面上的小车以速度 $V$ 前进。
如下图:
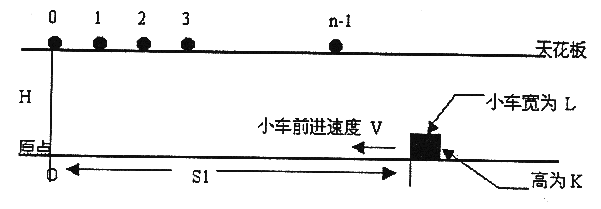
小车与所有小球同时开始运动,当小球距小车的距离 $\le 0.0001$ (感谢 Silver_N 修正) 时,即认为小球被小车接受(小球落到地面后不能被接受)。
请你计算出小车能接受到多少个小球。
输入格式
$H,S_1,V,L,K,n$($1 \le H,S_1,V,L,K,n \le 100000$)
输出格式
小车能接受到的小球个数。
样例 #1
样例输入 #1
5.0 9.0 5.0 2.5 1.8 5
样例输出 #1
1
思路
引用洛谷水友的话,就是希望你永远不要知道我是如何在信息学比赛上推物理公式的
不过不管是物理公式难度或是程序实现难度在提高组中都是签到题
这题的g给的很仁慈,因此可以直接得出车头t_min和车尾t_max时间和h、k之间的关系
通过对二者能够接住的最大值的位置和最小值位置相减,就能轻松得出个数
需要注意,最大距离不能大于总长度s1
代码
#include<stdio.h>
#include<cmath>
using namespace std;
int n;
double h,s1,v,l,k;
int main()
{
scanf("%lf %lf %lf %lf %lf %d",&h,&s1,&v,&l,&k,&n);
double t_max=sqrt(h/5);
double t_min=sqrt((h-k)/5);
int i_b=int(s1-t_min*v+l),i_e=int(s1-t_max*v);
i_b=min(i_b,n);i_e=max(i_e,0);
printf("%d",i_b-i_e);
}