题目描述
Scarlet 最近学会了一个数组魔法,她会在 n* n 二维数组上将一个奇数阶方阵按照顺时针或者逆时针旋转 90° 。
首先,Scarlet 会把 1 到 n^2 的正整数按照从左往右,从上至下的顺序填入初始的二维数组中,然后她会施放一些简易的魔法。
Scarlet 既不会什么分块特技,也不会什么 Splay 套 Splay,她现在提供给你她的魔法执行顺序,想让你来告诉她魔法按次执行完毕后的二维数组。
输入格式
第一行两个整数 n,m ,表示方阵大小和魔法施放次数。
接下来 m 行,每行 4 个整数 x,y,r,z ,表示在这次魔法中,Scarlet 会把以第 x 行第 y 列为中心的 2r+1 阶矩阵按照某种时针方向旋转,其中 z=0 表示顺时针, z=1 表示逆时针。
输出格式
输出 n 行,每行 n 个用空格隔开的数,表示最终所得的矩阵
样例 #1
样例输入 #1
5 4
2 2 1 0
3 3 1 1
4 4 1 0
3 3 2 1
样例输出 #1
5 10 3 18 15
4 19 8 17 20
1 14 23 24 25
6 9 2 7 22
11 12 13 16 21
提示
对于50%的数据,满足 r=1
对于100%的数据 1<= n,m<=500 ,满足 1<= x-r<= x+r<= n,1<= y-r<= y+r<= n 。
思路
一道简单(只肝1小时)的模拟题,关键在于找到行和列之间的关系,这里给大家贴两张直观的图
假设顺时针反转前一个矩阵长这样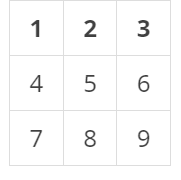
则反转后就变成了这样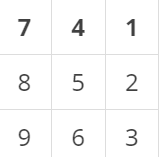
由此可以知道第a列原数据与第a行反转后数据相等。因此就很容易得到代码
void spin(int x,int y,int r)
{
for(int i=x-r;i<=x+r;i++)
{
for(int k=y-r;k<=y+r;k++)
temp[i][k]=square[i][k];
}//将以(x,y)为中心的(2r+1)*(2r+1)的矩阵赋给temp
int x1=x+r,y1=y-r;
for(int i=x-r;i<=x+r;i++)
{
for(int k=y-r;k<=y+r;k++)
{
square[i][k]=temp[x1][y1];//将某一列的数字赋值给某一列
x1--;
}
x1=x+r,y1++;
}
}
由此也可以知道逆时针反转的原理。
代码
#include<iostream>
#include<cstring>
using namespace std;
int square[505][505],temp[505][505];
void spin(int x,int y,int r)//顺时针旋转90°
{
for(int i=x-r;i<=x+r;i++)
{
for(int k=y-r;k<=y+r;k++)
temp[i][k]=square[i][k];
}
int x1=x+r,y1=y-r;
for(int i=x-r;i<=x+r;i++)
{
for(int k=y-r;k<=y+r;k++)
{
square[i][k]=temp[x1][y1];
x1--;
}
x1=x+r,y1++;
}
}
void spin_(int x,int y,int r)//逆时针旋转90°
{
for(int i=x-r;i<=x+r;i++)
{
for(int k=y-r;k<=y+r;k++)
temp[i][k]=square[i][k];
}
int x1=x-r,y1=y+r;
for(int i=x-r;i<=x+r;i++)
{
for(int k=y-r;k<=y+r;k++)
{
square[i][k]=temp[x1][y1];
x1++;
}
y1--,x1=x-r;
}
}
int main()
{
int n,m,t=0;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int k=1;k<=n;k++)
square[i][k]=++t;
}//首先给矩阵赋值
int x,y,r,z;
for(int i=0;i<m;i++)
{
cin>>x>>y>>r>>z;
if(z==0)
spin(x,y,r);
else if(z==1)
spin_(x,y,r);
}
for(int i=1;i<=n;i++)
{
for(int k=1;k<=n;k++)
cout<<square[i][k]<<" ";
cout<<endl;
}
}