记录部分题目
8:常规赛排名
描述
一场常规赛需要参赛双方进行至多三局游戏来决出胜者(先赢两局者胜)。
赢得一场常规赛可以为战队获取 1 个场次分,输掉一场常规赛则无事发生。
同时,每赢得一局游戏可以为战队获取 1 个游戏分,输掉一局游戏则会失去 1 个游戏分。
例如 TeamA 和 TeamB 的游戏结果是 2:1,那么本场比赛结束后,TeamA 获得 1 个场次分和 1 个游戏分,TeamB 只失去 1 个游戏分。
具体排名规则如下:
优先按照场次分高低排名,场次分相同的,则按照游戏分从高到低排名,仍然相同的,则按照战队名称的字典序从小到大排。
输入
第一行是一个正整数 n 表示总共的常规赛场次。(1 ≤ n ≤ 105)
接下来 n 行,每行包含两个字符串和一个比分,表示参赛双方的战况。
战队名称仅包含大小写字母且长度不超过 10,比分只会是 0:2、1:2、2:1、2:0 中的一个。
输出
按排名规则的顺序输出若干行,每行包括:战队名 场次分 游戏分。
样例输入
3
TeamA TeamB 2:1
TeamB TeamC 2:0
TeamA TeamC 1:2
样例输出
TeamB 1 1
TeamA 1 0
TeamC 1 -1
思路
这是一道模拟题,需要模拟比赛过程并统计每个队伍的分数。我们可以使用一个unordered_map来存储每个队伍的信息,使用一个结构体Team来表示每个队伍的名称、场次分和游戏分。对于每一场比赛,我们可以解析输入并根据比分更新每个队伍的信息。如果某个队伍赢了比赛,它的场次分和游戏分都会增加;如果它输了比赛,则它的游戏分会减少。
一旦我们统计了每个队伍的分数,我们可以将它们放入一个vector中,并使用一个compare函数对它们进行排序,以便根据场次分、游戏分和队伍名称的字典序输出排名。最后,我们遍历排好序的vector并输出每个队伍的信息。
总之,这道题的思路比较简单,重点在于正确解析输入并更新每个队伍的信息。我们需要考虑所有可能的比分情况,并使用一个unordered_map来快速查找每个队伍的信息。
代码
#include <iostream>
#include <vector>
#include <string>
#include <unordered_map>
#include <algorithm>
#include <sstream>
using namespace std;
struct Team {
string name;
int matches_won;
int game_points;
};
bool compare(const Team& a, const Team& b) {
if (a.matches_won == b.matches_won) {
if (a.game_points == b.game_points) {
return a.name < b.name;
}
return a.game_points > b.game_points;
}
return a.matches_won > b.matches_won;
}
int main() {
int n;
cin >> n;
cin.ignore();
unordered_map<string, Team> teams;
for (int i = 0; i < n; ++i) {
string line;
getline(cin, line);
istringstream iss(line);
string team1, team2;
char delimiter;
int score1, score2;
iss >> team1 >> team2 >> score1 >> delimiter >> score2;
if (score1 > score2) {
teams[team1].matches_won++;
teams[team1].game_points += (score1 - score2);
teams[team2].game_points -= (score1 - score2);
} else {
teams[team2].matches_won++;
teams[team2].game_points += (score2 - score1);
teams[team1].game_points -= (score2 - score1);
}
teams[team1].name = team1;
teams[team2].name = team2;
}
vector<Team> team_list;
for (const auto& team : teams) {
team_list.push_back(team.second);
}
sort(team_list.begin(), team_list.end(), compare);
for (const auto& team : team_list) {
cout << team.name << " " << team.matches_won << " " << team.game_points << endl;
}
return 0;
}
9:炉石传说-沉没之城
描述
小卢在玩某款卡牌游戏,每个回合中,他可以执行以下三种操作任意次。
1:抽牌,将牌库顶端的那张牌置入自己手牌的最右端
2:探底,将牌库底端的那张牌置于牌库顶端
3:沉没,将手牌中最左端的牌置于牌库底端
抽牌异常:当小卢执行抽牌操作时,系统会依次进行以下判断并只执行最先符合的那条。
1、如果此时牌库为空,那么这次抽牌操作会使小卢受到一次疲劳伤害。
2、如果此时手牌已满,那么这次抽牌操作会摧毁牌库顶端的那张牌。
疲劳伤害:初始值为 1,从第二次开始,每次疲劳伤害都比上一次多 1。
输入
第一行是三个不超过 104 的正整数 n、m、k 分别表示初始时牌库的数量,小卢操作的次数,小卢的手牌上限。
接下来一行 n 个不超过 104 的正整数表示从牌顶到牌底,每张卡牌的编号(可能会重复)。
最后一行 m 个 1 ~ 3 之间的数字,依次表示小卢本回合的操作。
输出
输出三行,第一行是小卢受到的疲劳伤害总和,第二行是小卢手牌中从左到右卡牌的编号,第三行是牌库中从顶到底卡牌的编号。
输出编号时,每两个编号用空格隔开,最后一个编号后面没有空格。
特别地,如果手牌为空或牌库为空,对应行需要输出一个empty。
样例输入
7 6 2
5 4 7 2 1 3 6
1 1 1 2 3 1
样例输出
0
4 6
2 1 3 5
提示说明
初始时手牌为空,抽第三张牌的时候,手牌已满,故编号为 7 的卡牌被摧毁。
思路
依旧是一道模拟题,需要模拟小卢玩卡牌游戏的操作过程。我们可以使用一个deque来表示牌库,一个vector来表示手牌。对于每个回合,我们需要执行给定的操作并根据规则更新牌库、手牌和疲劳伤害。
对于抽牌操作,我们需要注意两个特殊情况。如果牌库为空,小卢会受到疲劳伤害,并且疲劳伤害会递增;如果手牌已满,牌库顶端的牌会被摧毁。我们可以使用一个变量来表示疲劳伤害,和一个变量来表示当前的疲劳伤害值。
对于探底操作,我们可以使用deque的pop_back和push_front函数来实现。
对于沉没操作,我们可以使用vector的erase函数来删除手牌的第一个元素,并使用deque的push_back函数将它添加到牌库的末尾。
最后,我们可以根据题目要求输出疲劳伤害、手牌和牌库的编号。需要注意的是,如果手牌或牌库为空,我们需要输出empty。
总之,这道题的思路比较简单,需要注意一些细节。在实现时,我们可以使用deque来处理牌库和探底操作,使用vector来处理手牌和沉没操作。
代码
#include <iostream>
#include <deque>
#include <vector>
using namespace std;
int main() {
int n, m, k;
cin >> n >> m >> k;
deque<int> deck;
for (int i = 0; i < n; i++) {
int card;
cin >> card;
deck.push_back(card);
}
vector<int> actions(m);
for (int i = 0; i < m; i++) {
cin >> actions[i];
}
vector<int> hand;
int fatigue_damage = 0;
int fatigue_counter = 1;
for (int action : actions) {
if (action == 1) {
if (deck.empty()) {
fatigue_damage += fatigue_counter;
fatigue_counter++;
} else {
if (hand.size() < k) {
hand.push_back(deck.front());
deck.pop_front();
} else {
deck.pop_front();
}
}
} else if (action == 2) {
if (!deck.empty()) {
deck.push_front(deck.back());
deck.pop_back();
}
} else if (action == 3) {
if (!hand.empty()) {
deck.push_back(hand.front());
hand.erase(hand.begin());
}
}
}
cout << fatigue_damage << endl;
if (hand.empty()) {
cout << "empty" << endl;
} else {
for (size_t i = 0; i < hand.size(); i++) {
cout << hand[i] << (i + 1 == hand.size() ? '\n' : ' ');
}
}
if (deck.empty()) {
cout << "empty" << endl;
} else {
for (size_t i = 0; i < deck.size(); i++) {
cout << deck[i] << (i + 1 == deck.size() ? '\n' : ' ');
}
}
return 0;
}
11:公约树
描述
自定义一棵公约树,它或是一棵空树,或是具有以下性质的二叉树:
对于任意一个节点,若它拥有左孩子,则左孩子与它互质;若它拥有右孩子,则右孩子与它不互质;它的左右子树也分别是公约树。
在向一颗公约树添加元素时,如果该树为空,则新建一个值等于该元素的节点。
如果该树不为空,则需要将这个元素与根节点进行比较,如果互质,则将该元素添加至其左子树,否则将该元素添加至其右子树。
现在给你一个序列,请你按照给定顺序添加元素,最后输出这棵树的中序遍历结果。
输入
第一行是一个正整数 n 表示序列的长度。(1 ≤ n ≤ 100)
接下来 n 个不超过 109 的正整数表示序列每个元素的大小。
输出
在一行中输出这棵树的中序遍历结果,每两个元素之间用空格隔开,最后一个元素后面没有空格。
样例输入
6
6 5 2 1 3 4
样例输出
1 5 6 3 2 4
提示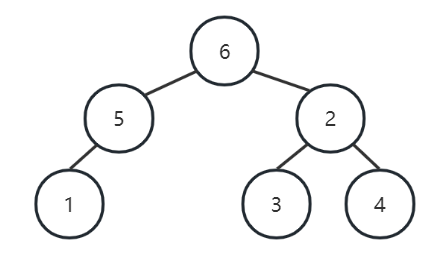
思路
题目要求实现一个自定义的公约树,这棵树要么为空,要么具有如下性质:对于任意一个节点,如果它有左孩子,则左孩子与它互质,如果它有右孩子,则右孩子与它不互质,它的左右子树也分别是公约树。
为了实现这个数据结构,首先定义一个节点结构体 Node,它包含一个整数值 value,以及指向左右子树的指针 left 和 right。
接下来,我们定义了一个 createNode 函数,用于创建一个新的节点。该函数接受一个整数值作为参数,并返回一个新的节点指针。
为了判断两个数是否互质,定义一个 isCoprime 函数。该函数接受两个整数作为参数,并返回一个布尔值。如果这两个数互质,则返回 true;否则返回 false。该函数使用了欧几里得算法来计算两个数的最大公约数。
为了将元素插入到公约树中,再定义 insert 函数。该函数接受一个指向节点指针的指针和一个整数值作为参数。如果根节点为空,则创建一个新的节点作为根节点。否则就需要将该元素与根节点进行比较。如果它们互质,则将该元素插入到左子树中;否则将其插入到右子树中。
最后定义 inorderTraversal 函数,用于中序遍历公约树并输出排序后的结果。该函数接受一个指向节点的指针和一个布尔值 isFirst 作为参数。它先遍历左子树,然后输出节点的值。在输出节点的值之前,它会检查 isFirst 的值,如果是第一个被输出的元素,则不输出空格,否则输出一个空格。接着遍历右子树。
代码
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
// 定义节点结构体
typedef struct Node {
int value;
struct Node* left;
struct Node* right;
} Node;
// 创建新节点
Node* createNode(int value) {
Node* node = (Node*) malloc(sizeof(Node));
node->value = value;
node->left = NULL;
node->right = NULL;
return node;
}
// 判断两个数是否互质
bool isCoprime(int a, int b) {
if (a == 1 || b == 1) {
return true;
}
if (a % b == 0) {
return (b == 1);
}
return isCoprime(b, a % b);
}
// 插入元素
void insert(Node** root, int value) {
if (*root == NULL) {
// 如果根节点为空,则创建新节点作为根节点
*root = createNode(value);
} else {
// 比较插入元素和根节点的互质性
if (isCoprime(value, (*root)->value)) {
// 如果插入元素和根节点互质,则插入到左子树中
insert(&((*root)->left), value);
} else {
// 如果插入元素和根节点不互质,则插入到右子树中
insert(&((*root)->right), value);
}
}
}
// 中序遍历公约树并输出排序后的结果
void inorderTraversal(Node* root, bool* isFirst) {
if (root != NULL) {
inorderTraversal(root->left, isFirst);
if (*isFirst) {
*isFirst = false;
} else {
printf(" ");
}
printf("%d", root->value);
inorderTraversal(root->right, isFirst);
}
}
int main() {
int n;
scanf("%d", &n);
Node* root = NULL;
for (int i = 0; i < n; i++) {
int value;
scanf("%d", &value);
insert(&root, value);
}
bool isFirst = true;
inorderTraversal(root, &isFirst);
return 0;
}