2024第三次线上赛wp

MISC

卫继龚的日常

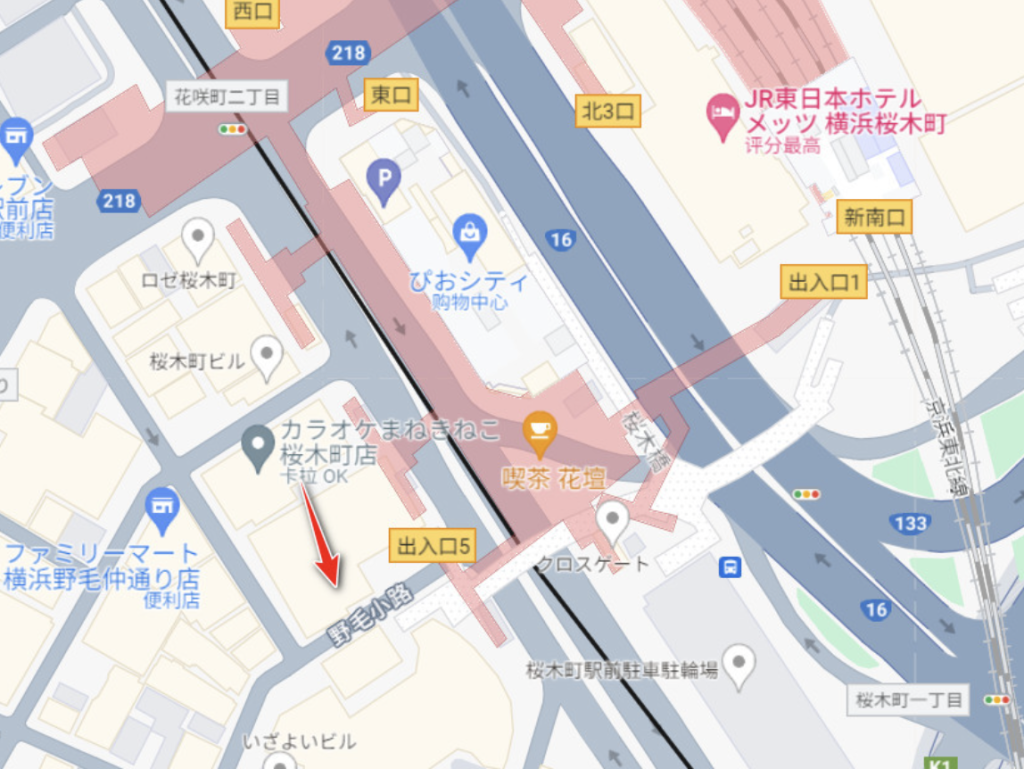
将题目中的图片抠出来，放进谷歌，识别出是日本横滨北仲桥。

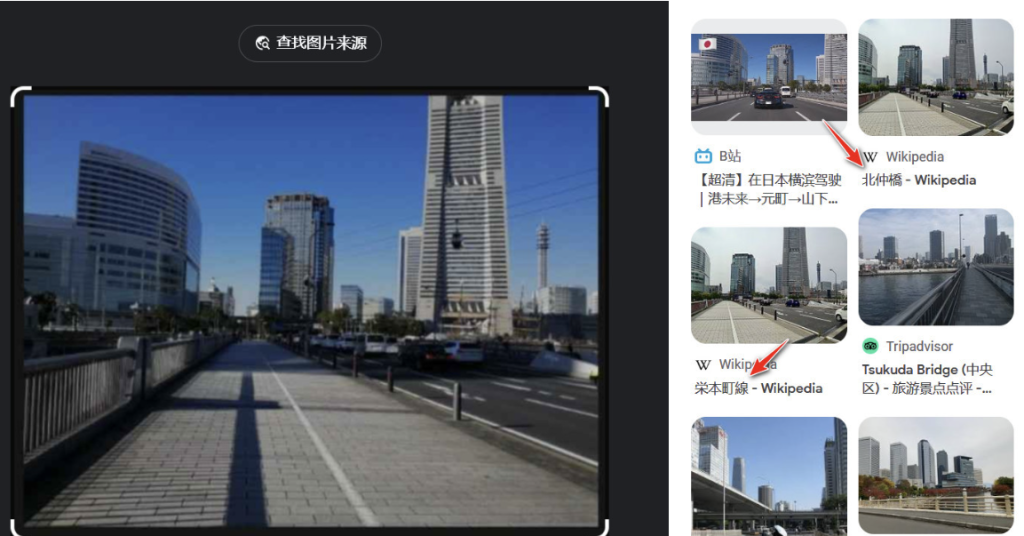
根据题意附近应该有JR地铁站，继续谷歌地图，发现附近有JR樱木町站。

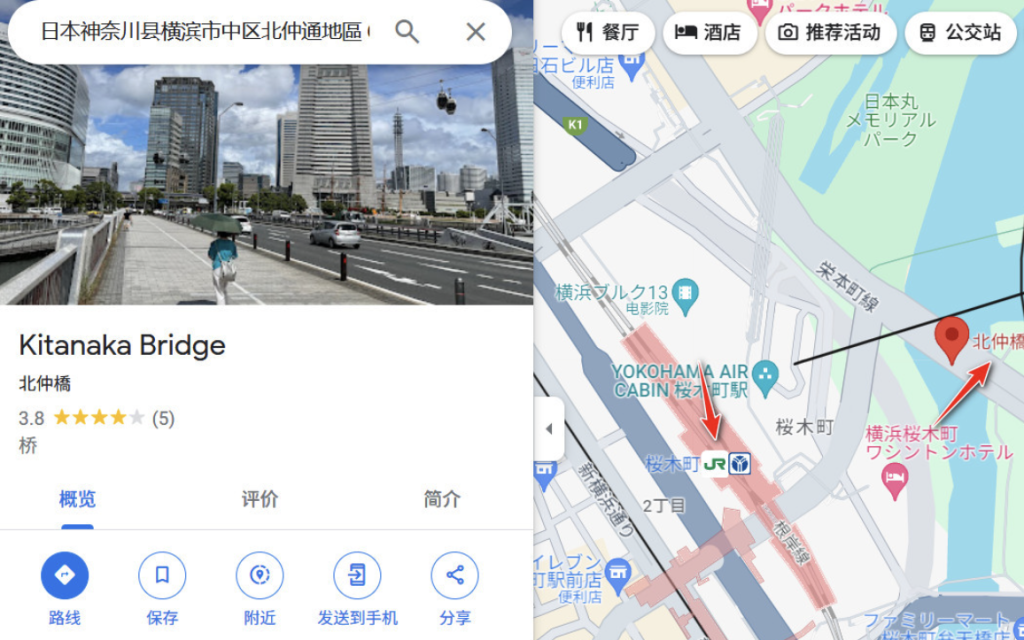
根据题意，接着找附近的商店街。谷歌一下，附近有野毛小路商店街。

同时寻找日本知名的一元店，百度到了几个日本知名品牌。

如果你是这样做或是以类似思路做的，那么此时你的思路和寻找方向已经偏了。

最关键的原因，还是审题不完全。关键词：5分钟就能到地铁。仔细看题目图片，假设图片是在上下班路途上拍的，那么他必然要经过北仲桥。如果他是从家到地铁经过的北仲桥，那么他家附近的商店街应该在北仲桥附近，而野毛商店街的位置是相反方向。也就是说我应该去找北仲桥附近的商店街，但是找了一圈，没有发现很知名的商店街。

此时，假如北仲桥是在作者公司附近呢？樱木町站是作者公司附近的地铁站，因此题目图片中，加了一句：“只需要坐5分钟地铁”。

以樱木町站为起点，5分钟的车程，大致1-2站。继续谷歌，找到JR东日本的路线图。

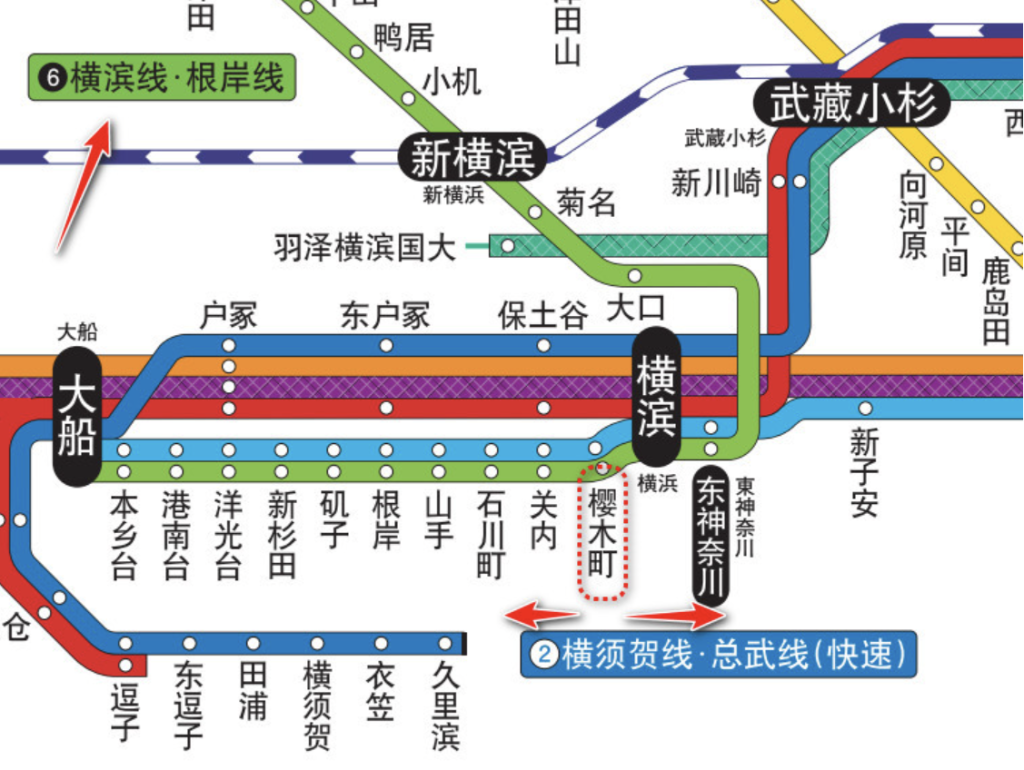
根岸线樱木町站，5分钟车程，前后不会超过2站，分别是石川町、关内、横滨、东神奈川。

以这4个站，再结合谷歌出来的横滨知名商店街

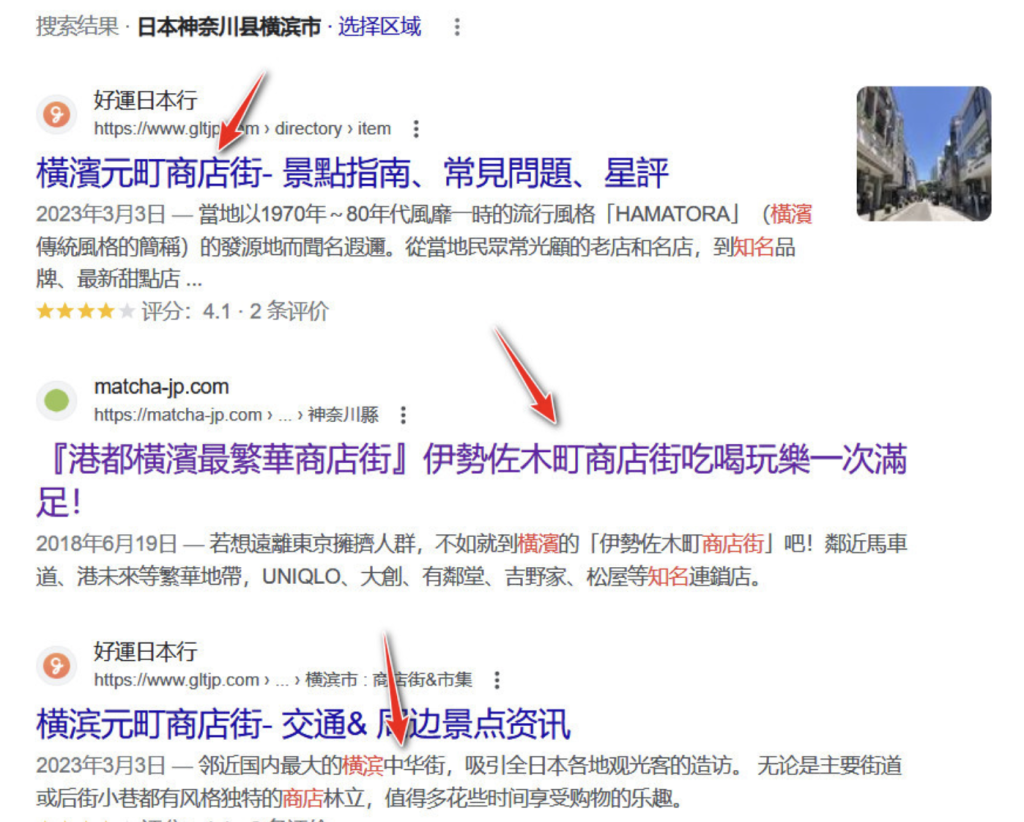
继续谷歌地图

在横滨站附近寻找，一无所获

关内站附近发现伊势佐木町商店街。

依次谷歌日本知名的百元品牌，输入CanDo终于发现目标

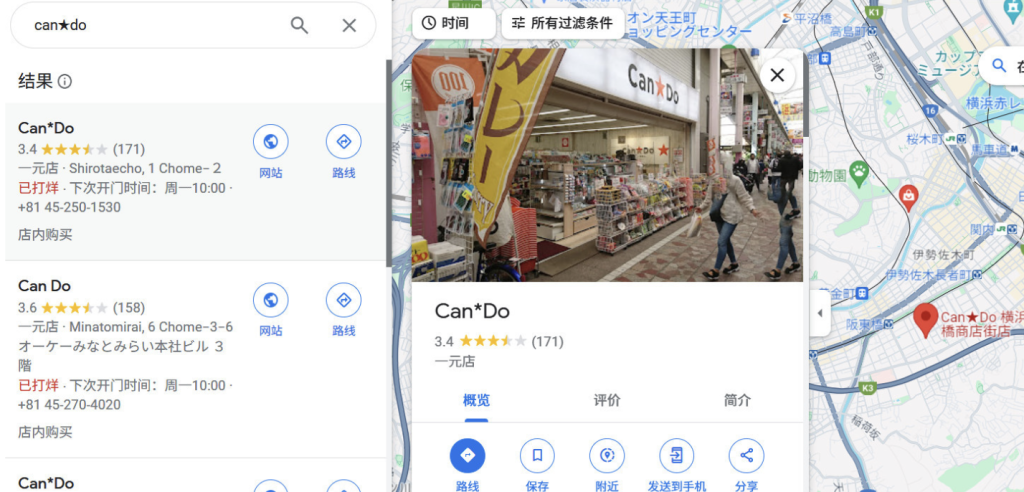
使用谷歌街景

Project-X

题目给了一个 pcapng 的流量包文件，在分析前先来过一下Vmess协议下数据包加密过程（官方配置文档、通信协议文档）

假设有如下网络拓补

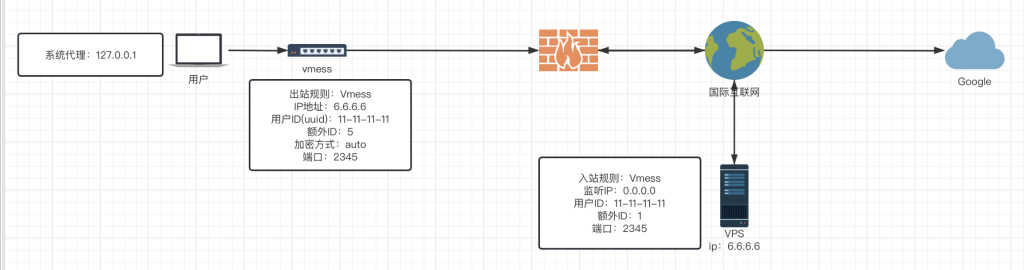
此时用户在配置好代理软件后使用vmess协议进行通信，在浏览器中使用google，发起了一个下面这样的数据包（1.1.1.1是用户ip，1145是用户发起请求端口）

为了方便画图，以上数据包所有内容都包含在请求包体中。此时数据包会被交给代理软件，vmess协议会在数据包前加上一个用来加密该数据包的加密方式

vmess允许用户自定义加密包体的方式，一般会在配置页面选择auto。这里我们假设使用AES-128-GCM加密，这样请求包体的内容就会被加密成无规则的字节流，被加密后包体就变成这样（遮挡部分表示被加密，后面使用的颜色不同表示加密方式不同）

接着会根据用户在配置文件中使用的用户id进行AES-128-CFB加密，将包体加密方式这部分也加密起来（下面是官方文档给的加密方式，看不懂也没事，只要知道会用一个特定的值与用户id进行加密运算，将这部分给搞糊）

并且会在前面加上当前时间戳与用户id的md5值作为一个验证值，此时整个数据包就是这个样子

最后拼接上代理服务器的ip地址与端口，就变成了这样

当数据包来到防火墙时，由于请求包体被完全加密，防火墙无法识别出用户意图，且代理服务器不在防火墙黑明单，于是就会放行数据包。代理服务器拿到数据包后，会先开一个大小为30～90左右的数组，对当前时间戳的+-30秒进行逐个的md5校验，当数据包中携带的校验值与数组中某个值匹配后，就会认定该数据包为有效数据包，于是对后面被加密的两个部分进行解密。解密后就重新拿到了下面这个数据包

接着再进行一层解密，就能得到我们的请求意图。这便是最原始的vmess协议通信过程。这里有一个配置信息我们没有说到，就是额外id。其实额外id的存在就是为了防止在同一时间段内发送大量数据包导致校验值重复，比如原本校验值是md5(11451)，当额外id为1时就有md5(11452)，以此类推。但这种验证方式也有局限性，在实际使用中已被发现存在被重放攻击的风险，具体可以看这篇，下面是官方文档对这一风险的应对手段

VMessMD5 被弃用的原因是因为它能够被很容易地通过主动探测的手段检测到，见上面提到的那篇 v2ray-core#2523。

简单来说就是使用AEAD认证的方式取代我们上述的md5验证值。这样即便防火墙试图修改被加密的数据包，被修改的数据包发送到代理服务器后也会被丢弃，就能避免重放攻击的风险。置方式也很简单，就是将额外id设置为0。而在最新版v2ray-core中，已经对vmess协议强制使用AEAD认证

介绍完vmess协议的通信原理后，再来看看赛题。这道题就是AEAD 的加密方式

用wireshark翻流量可以得到一个 v2ray 的 json 配置文件，也是从这里确定了是VMess流量分析

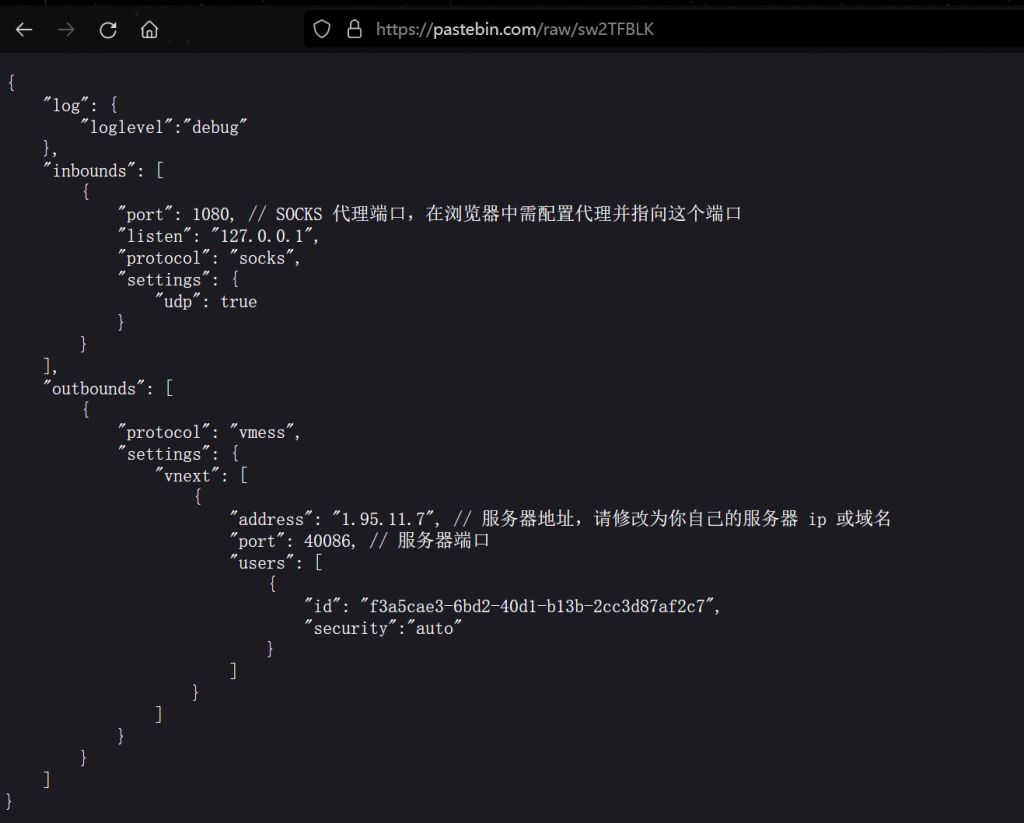
解密流量有两种方法，一种是通过阅读代码来自己实现解密，另一种是通过重放流量来获取明文。

关于协议的部分实现，可以参考 extra-VMessAEADdoc.zip 但是协议的最终实现还是需要参考 v2ray-core 的源码，因为有些地方的实现和文档中的描述不一致。

这里我们可以使用一个专门用来解析AEAD认证的库，并使用其编写一段exp

import uuid

from vmess_aead.encoding import VMessBodyEncoder
from vmess_aead.headers.request import VMessAEADRequestPacketHeader
from vmess_aead.utils.reader import BytesReader

data = "a49502ee07ffdd20f11597e961f7768b41be7bc32030107fc81f235f72ff1b294d074ade94281242412b4c19123b15250ac3d5ad9524df9acd0ee5f6dcca7b0c2849b2f4df20190dd084c01c3f6e2834dd87cb8e97fa178b2ec454755f89d9b735ae6dab9c7989cf4154f7eae53774d9d6cdb55d0a76fdaf21e08bae26e49cbb3c56d11a3fe540454bfbae06305460301caca4109df3335b0c3646b6e2d856a927f9298b87da3a7cf3cffcca6c27259fc055faa9f3155cc95f698bb37436008783b6cd03d38a8e109f78a48c860b600fcbe825cd6c6a5be2c95fce121df574c70fe62e4f24e28de5983db6c3c0192d72ec785b6d58c4b8301c4f70eab683"
data = bytes.fromhex(data)

reader = BytesReader(data)
user_id = uuid.UUID("f3a5cae3-6bd2-40d1-b13b-2cc3d87af2c7")


header = VMessAEADRequestPacketHeader.from_packet(reader, user_id)
print(header)

encoder = VMessBodyEncoder(
    header.payload.body_key,
    header.payload.body_iv,
    header.payload.options,
    header.payload.security,
    header.payload.command,
)
body = encoder.decode_once(reader)
print(body)

在比赛中，重放流量应当是更加简单的方法。

Tip：因为 VMessAEAD 并没有类似于 VMessMD5 那样的请求头时间戳爆破机制，只有检查根据 UUID 最终解密后的结果中时间戳是否在合理范围内的机制。所以重放流量是行得通的，只需要 Patch 掉对时间范围的检查即可。

解析了流量中的数据后可以得到一个图片的地址：https://p.sda1.dev/16/11c111ee40a928d5d751dd5869414093/__p0.png

用 zsteg 扫就能发现图片末尾有一个压缩包，或者也可以用binwalk。用 foremost 提取出来后可以发现需要密码

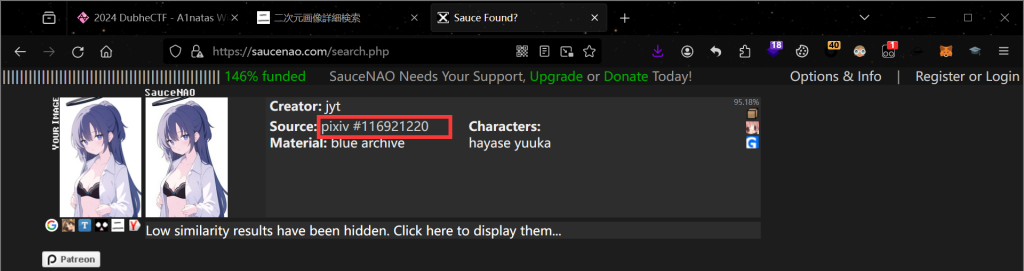
观察到图片文件命名为 __p0.png，我们可以联想到这张图片的原始文件名可能是 <某个数字id>_p0.png。这里可以去 saucenao 搜这个图片，我们可以找到原始图片的文件名为 116921220_p0，所以压缩包的密码猜测是116921220

解压压缩包后得到一个项目的源码
后面的考点就主要是 Web 方向的了—— EdTunnel，Wrangler 和 SSRF

这部分开始就是 Web 的部分了。

观察 docker-compose.yml，我们可以看到一个名为 edtunnel 的服务。Flag 存在于 Worker 的env变量中。

EdTunnel 部分是来自 https://github.com/3Kmfi6HP/EDtunnel 的代码，只对 UUID 和默认路由进行了简单的修改。

可以看到，EdTunnel 是通过 Wrangler 本地的开发模式部署的，查看 Wrangler 的 GitHub，可以发现 CVE-2023-7080，这个漏洞描述了 Wrangler 的 Inspector 端口是对所有接口监听的，所以攻击者可以在临近网络上访问到 Inspector 端口从而实现 Worker 沙盒内的远程代码执行。

虽然题目版本的 Wrangler 已经修复了这个漏洞，但是由于这个代码的作用是使用 Cloudflare Worker 的 API 实现一个 VLESS over WebSocket 的代理，所以我们可以通过这个代理来 SSRF 到部署 EdTunnel 的容器，从而实现连接到 Inspector 的端口。

具体建立连接将 V8 Inspector 端口暴露到本地的配置文件可以参考 exp-config.json，使用 v2ray run -c exp-config.json -format jsonv5 命令来运行。（因为 V4 版本的 V2Ray 对传输层流量多层代理支持不佳）

将端口暴露到本地后，我们可以在 Chrome 的 DevTools 中直接连接到这个端口（左上会出现 Node.js 的标识）。在 DevTools 的 Memory Snapshot 中，我们可以打出 Heap Snapshot，然后在其中搜索关键字即可找到 Flag 变量

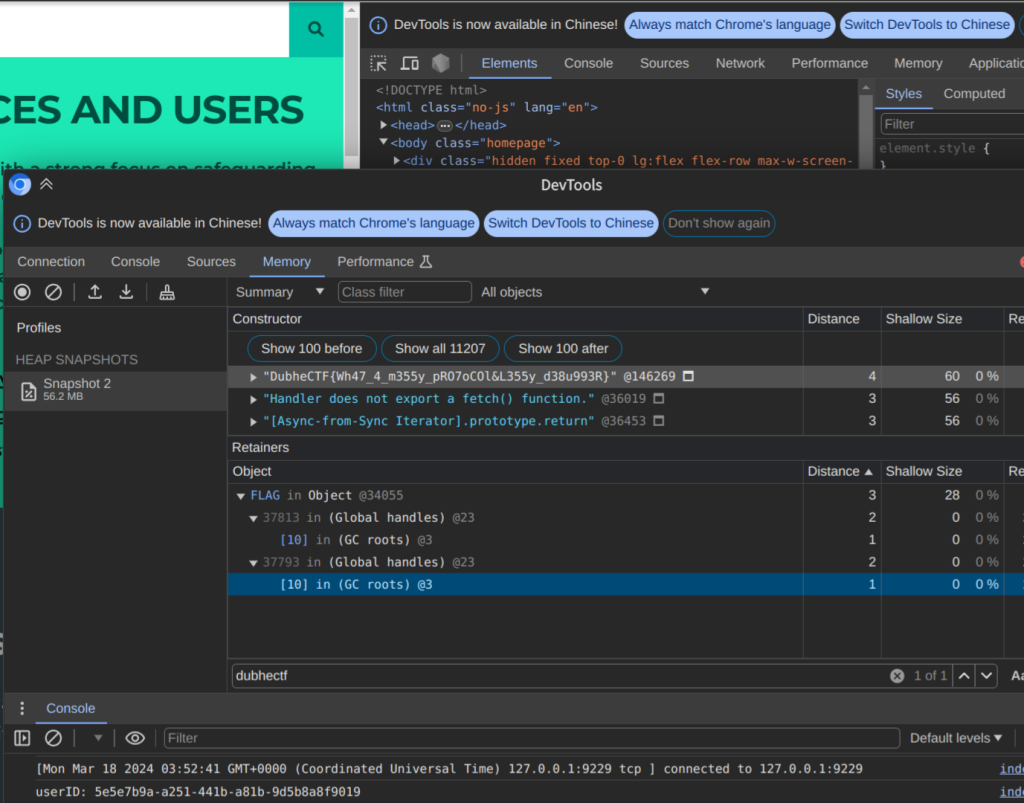
RAW标志

使用rawpy获取相机图像的原始RAW数据

其实就是一个LSB提最低位数据

可以先用exiftool查看一下图像数据的偏移

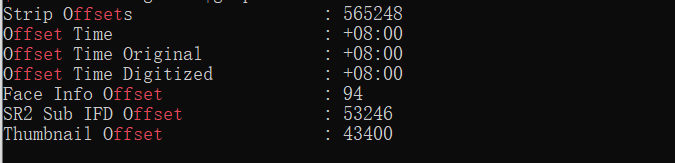
可知偏移是565248，就是在整个图片文件中从565248字节开始才是图片的数据，隐写从这里开始

而官方wp说Uncompressed RAW每个Sample记录了14Bits的数据，放在了一个short里面，而且用的是小端序来存储，所以使用struct.unpack()来解包图片数据struct.unpack('<'+f'{width*height}H', raw_data)，<是指小端序，H是指unsigned short

对于raw数据，有特定的函数进行处理图像数据

利用rawpy库的raw_image_visible可以获取原始数据

然后提取lsb即可

import rawpy

with rawpy.imread('image.ARW') as raw:
    rgb = raw.postprocess()
    #print(rgb)
    data = raw.raw_image_visible[0]
    #print(data)
    data= ''.join(map(str,data & 0x01))
    print(data)
"""
[[[ 69  79  93]
  [ 69  79  93]
  [ 69  79  94]
  ...
  [ 62  73  92]
  [ 62  72  93]
  [ 61  73  93]]
  """

得到二进制数据，Cyber处理一下得到flag

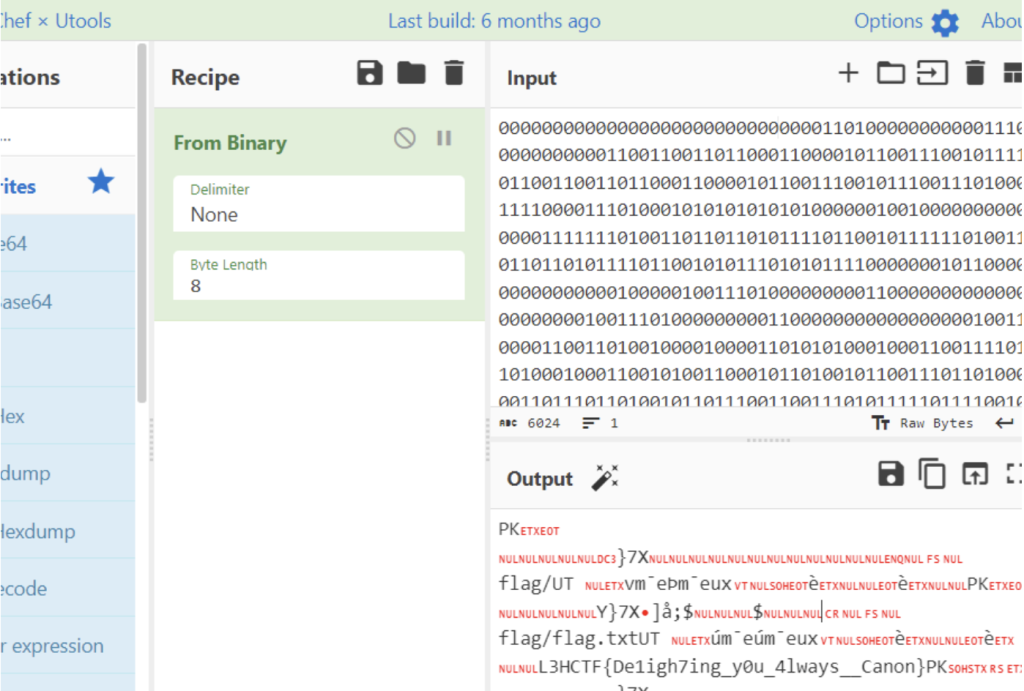
svg

svg 格式，base64 转文件，steghide 爆破

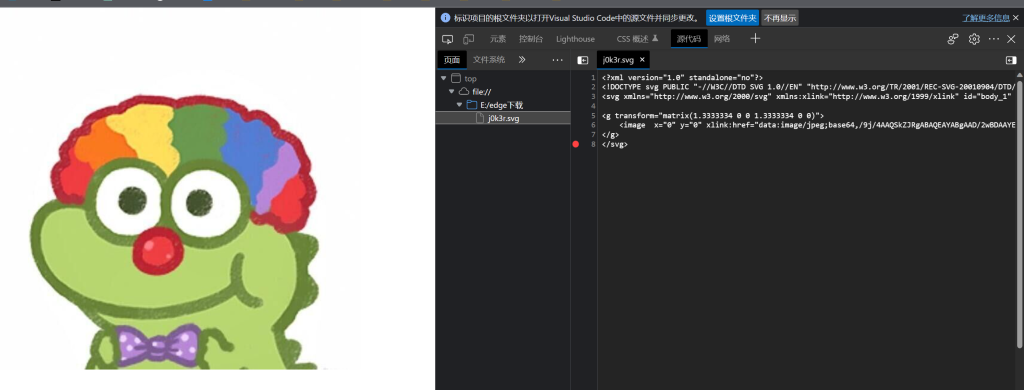
打开看到源码处有base64编码，提取出来

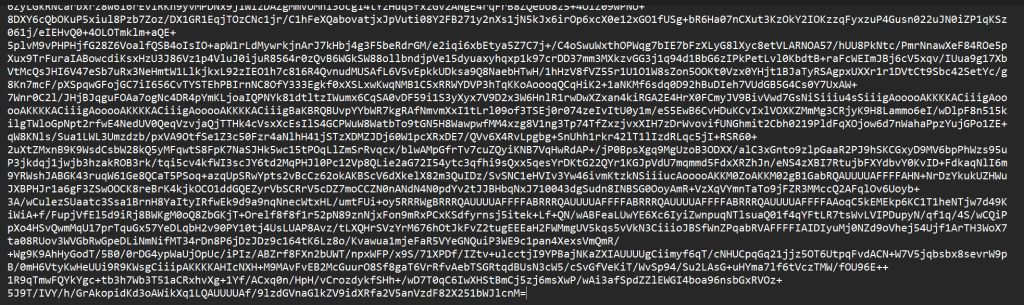
放入在线网站转换

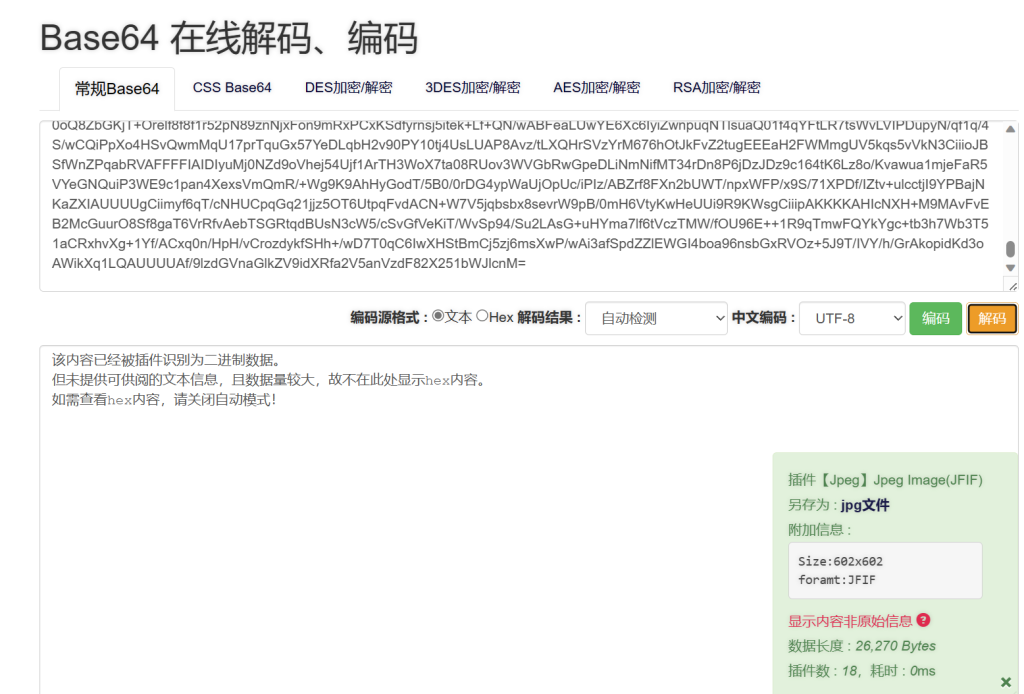
保存jpg文件，010查看

保存jpg文件到kali，steghide本身没有爆破功能，这里使用stegseek爆破

CRYPTO

rlwe

f = x^N - 1上存在问题，f可以分解为多个多项式相乘，f可以分为多个因子，于是降低degree使用LLL算法求出s关于不同f因子的余数，再使用crt求解，由于s最大度数不超过64，于是只需要求解f中度数小于64的因子即可

from time import time
from Crypto.Util.number import *
from sage.all import *
from subprocess import check_output
from re import findall

q = 1219077173
F.<x> = Zmod(q)[]
N = 1024
x = F.gen()
f = x^N - 1

a = 216047404*x^1023 + 1008199117*x^1022 + 39562072*x^1021 + 189992355*x^1020 + 1087671639*x^1019 + 541371337*x^1018 + 1146044200*x^1017 + 212969175*x^1016 + 1114159572*x^1015 + 1112032860*x^1014 + 1204883609*x^1013 + 1181544913*x^1012 + 851496082*x^1011 + 222877006*x^1010 + 163176236*x^1009 + 268697504*x^1008 + 613151090*x^1007 + 1185245256*x^1006 + 215725010*x^1005 + 789898500*x^1004 + 1156619111*x^1003 + 610859911*x^1002 + 959814483*x^1001 + 684353251*x^1000 + 290850651*x^999 + 675880502*x^998 + 836239751*x^997 + 487296407*x^996 + 778816128*x^995 + 1013639221*x^994 + 189137575*x^993 + 172217836*x^992 + 572872008*x^991 + 865759581*x^990 + 399805736*x^989 + 394587004*x^988 + 633085719*x^987 + 15142893*x^986 + 461176831*x^985 + 1078060208*x^984 + 787396508*x^983 + 877420202*x^982 + 1121486845*x^981 + 146921816*x^980 + 670134387*x^979 + 574407635*x^978 + 1148395437*x^977 + 748514947*x^976 + 970442995*x^975 + 280085063*x^974 + 420670822*x^973 + 20159574*x^972 + 219680665*x^971 + 401202858*x^970 + 328444623*x^969 + 623312316*x^968 + 917712264*x^967 + 588061576*x^966 + 625482841*x^965 + 220929234*x^964 + 778461001*x^963 + 498203565*x^962 + 1055981771*x^961 + 70562147*x^960 + 931081750*x^959 + 93569863*x^958 + 314876311*x^957 + 932364613*x^956 + 1132016772*x^955 + 371703330*x^954 + 189301560*x^953 + 739232608*x^952 + 916695967*x^951 + 399818344*x^950 + 558604923*x^949 + 1092603913*x^948 + 987195616*x^947 + 665679589*x^946 + 1142632478*x^945 + 198797278*x^944 + 110832477*x^943 + 775688737*x^942 + 275416086*x^941 + 435656120*x^940 + 754150483*x^939 + 1024583186*x^938 + 972075461*x^937 + 1071060217*x^936 + 710789980*x^935 + 691361770*x^934 + 1097024307*x^933 + 862356288*x^932 + 354500195*x^931 + 158151296*x^930 + 733475281*x^929 + 215008492*x^928 + 151139272*x^927 + 1000425669*x^926 + 590964357*x^925 + 373950911*x^924 + 43038800*x^923 + 338044906*x^922 + 293954870*x^921 + 393479*x^920 + 555095359*x^919 + 418829106*x^918 + 95391760*x^917 + 897658305*x^916 + 1040609125*x^915 + 239948276*x^914 + 1190720461*x^913 + 160498737*x^912 + 394967890*x^911 + 104302686*x^910 + 48021969*x^909 + 761000569*x^908 + 356140410*x^907 + 225246587*x^906 + 79172445*x^905 + 975365689*x^904 + 1077396491*x^903 + 728717352*x^902 + 964273647*x^901 + 258781036*x^900 + 746930481*x^899 + 793742220*x^898 + 542128050*x^897 + 562413014*x^896 + 701216258*x^895 + 928704966*x^894 + 98656502*x^893 + 1016152774*x^892 + 140544845*x^891 + 226416702*x^890 + 309310359*x^889 + 519065123*x^888 + 346740110*x^887 + 116615122*x^886 + 990804519*x^885 + 208648062*x^884 + 605381435*x^883 + 821163414*x^882 + 864698754*x^881 + 424773230*x^880 + 1184139330*x^879 + 437390254*x^878 + 41435781*x^877 + 824197241*x^876 + 1181823353*x^875 + 354135255*x^874 + 921600154*x^873 + 972782404*x^872 + 304175744*x^871 + 976950586*x^870 + 561195955*x^869 + 840601911*x^868 + 848362310*x^867 + 698380233*x^866 + 703722831*x^865 + 527081934*x^864 + 996708932*x^863 + 926257884*x^862 + 113808466*x^861 + 111022399*x^860 + 336240881*x^859 + 281602555*x^858 + 456022351*x^857 + 303940681*x^856 + 1152960332*x^855 + 762827305*x^854 + 1097893502*x^853 + 1159492861*x^852 + 791288185*x^851 + 552596428*x^850 + 1160303133*x^849 + 855459983*x^848 + 870046128*x^847 + 412042730*x^846 + 527317697*x^845 + 118258027*x^844 + 1156090191*x^843 + 1184418516*x^842 + 736914609*x^841 + 1042440949*x^840 + 1118336201*x^839 + 692314475*x^838 + 888141647*x^837 + 611975215*x^836 + 112482309*x^835 + 774541929*x^834 + 877613260*x^833 + 218484596*x^832 + 744043072*x^831 + 1149426359*x^830 + 1086732941*x^829 + 218727414*x^828 + 111004493*x^827 + 48035668*x^826 + 1129753198*x^825 + 410088959*x^824 + 1186919074*x^823 + 291266088*x^822 + 622780685*x^821 + 908030149*x^820 + 152548456*x^819 + 970996704*x^818 + 643233117*x^817 + 97648457*x^816 + 167039372*x^815 + 451159004*x^814 + 21522258*x^813 + 446568222*x^812 + 97236135*x^811 + 601480363*x^810 + 896523050*x^809 + 635312918*x^808 + 771155729*x^807 + 727217487*x^806 + 1103325662*x^805 + 1145702253*x^804 + 111451279*x^803 + 709647761*x^802 + 155865734*x^801 + 788861657*x^800 + 25328658*x^799 + 387592047*x^798 + 631380316*x^797 + 195654331*x^796 + 379901017*x^795 + 110746571*x^794 + 821639667*x^793 + 1196705497*x^792 + 926725497*x^791 + 752090468*x^790 + 565928514*x^789 + 107924077*x^788 + 1035444397*x^787 + 389590222*x^786 + 746022468*x^785 + 1152494936*x^784 + 1047183126*x^783 + 935173423*x^782 + 237022259*x^781 + 68211471*x^780 + 682392084*x^779 + 900610142*x^778 + 659697118*x^777 + 381789469*x^776 + 895479393*x^775 + 342674862*x^774 + 1034152415*x^773 + 736863278*x^772 + 233824501*x^771 + 511543257*x^770 + 43539547*x^769 + 871109943*x^768 + 234226499*x^767 + 958639125*x^766 + 913885377*x^765 + 757234386*x^764 + 330354514*x^763 + 693659124*x^762 + 46757147*x^761 + 24910108*x^760 + 263754046*x^759 + 1007999117*x^758 + 569158879*x^757 + 781185896*x^756 + 328234792*x^755 + 1166796778*x^754 + 1023882729*x^753 + 1126014838*x^752 + 412948341*x^751 + 745762031*x^750 + 184601330*x^749 + 1195686854*x^748 + 226180761*x^747 + 813440273*x^746 + 198496604*x^745 + 646284299*x^744 + 775658802*x^743 + 1051631440*x^742 + 382010443*x^741 + 884529292*x^740 + 1171509241*x^739 + 148470016*x^738 + 545551560*x^737 + 895321797*x^736 + 990533556*x^735 + 1006826878*x^734 + 444425261*x^733 + 538658289*x^732 + 1201448839*x^731 + 813543244*x^730 + 866138640*x^729 + 992484781*x^728 + 797592952*x^727 + 5350520*x^726 + 1088776239*x^725 + 1011384293*x^724 + 202279961*x^723 + 580990742*x^722 + 608736084*x^721 + 592191483*x^720 + 603821965*x^719 + 686032966*x^718 + 309449994*x^717 + 997796743*x^716 + 323694959*x^715 + 404631321*x^714 + 684041814*x^713 + 954922509*x^712 + 17334061*x^711 + 1038027065*x^710 + 189030167*x^709 + 238786122*x^708 + 854157242*x^707 + 857322405*x^706 + 847505723*x^705 + 531600098*x^704 + 413144959*x^703 + 150862275*x^702 + 176120020*x^701 + 147651128*x^700 + 20961937*x^699 + 924892688*x^698 + 207889399*x^697 + 506289209*x^696 + 201657090*x^695 + 866897606*x^694 + 282950189*x^693 + 484625027*x^692 + 720969770*x^691 + 557487808*x^690 + 664292309*x^689 + 667236796*x^688 + 505039446*x^687 + 636507041*x^686 + 717904854*x^685 + 742491214*x^684 + 235380401*x^683 + 885103138*x^682 + 227708439*x^681 + 195450351*x^680 + 914408549*x^679 + 890140153*x^678 + 959662247*x^677 + 655663410*x^676 + 682768547*x^675 + 1063757282*x^674 + 776284911*x^673 + 1114588219*x^672 + 689022198*x^671 + 1160585767*x^670 + 784564493*x^669 + 599804982*x^668 + 954265199*x^667 + 1160092910*x^666 + 1178991310*x^665 + 610146522*x^664 + 589028938*x^663 + 972903553*x^662 + 933544074*x^661 + 910101746*x^660 + 1199479046*x^659 + 129564572*x^658 + 16630574*x^657 + 604268174*x^656 + 905616984*x^655 + 229755095*x^654 + 543777663*x^653 + 880642044*x^652 + 750742780*x^651 + 801027824*x^650 + 59869899*x^649 + 178293151*x^648 + 413473523*x^647 + 790966353*x^646 + 36947608*x^645 + 215402931*x^644 + 198271237*x^643 + 394503398*x^642 + 933396244*x^641 + 764498758*x^640 + 960831635*x^639 + 710558646*x^638 + 160491214*x^637 + 161213508*x^636 + 932611994*x^635 + 226519192*x^634 + 554464756*x^633 + 82595536*x^632 + 1144714763*x^631 + 361090580*x^630 + 747809061*x^629 + 114293244*x^628 + 253349999*x^627 + 1051279816*x^626 + 1079507344*x^625 + 864605458*x^624 + 1100098300*x^623 + 323233106*x^622 + 1070769430*x^621 + 1048471132*x^620 + 23281664*x^619 + 1099148878*x^618 + 812556000*x^617 + 452606567*x^616 + 892217880*x^615 + 741556204*x^614 + 37168552*x^613 + 286980867*x^612 + 1125383508*x^611 + 782814488*x^610 + 1214851511*x^609 + 270577673*x^608 + 364433480*x^607 + 825553809*x^606 + 589475297*x^605 + 293114041*x^604 + 1115978872*x^603 + 21831218*x^602 + 856821602*x^601 + 213782489*x^600 + 287159884*x^599 + 1015101950*x^598 + 494211644*x^597 + 38143731*x^596 + 882805771*x^595 + 721674528*x^594 + 120092153*x^593 + 636819567*x^592 + 365557574*x^591 + 619653423*x^590 + 1207892829*x^589 + 971282528*x^588 + 379459809*x^587 + 507124241*x^586 + 1050378769*x^585 + 113715629*x^584 + 841835564*x^583 + 1055649818*x^582 + 904319486*x^581 + 83232231*x^580 + 282044435*x^579 + 11563226*x^578 + 283283452*x^577 + 515932154*x^576 + 415242679*x^575 + 686396058*x^574 + 414011723*x^573 + 22692318*x^572 + 593039855*x^571 + 42054428*x^570 + 242713788*x^569 + 756543053*x^568 + 297264974*x^567 + 656668981*x^566 + 103185189*x^565 + 279211827*x^564 + 66472175*x^563 + 221289056*x^562 + 418547255*x^561 + 587378319*x^560 + 781217899*x^559 + 828907515*x^558 + 1026785730*x^557 + 936576598*x^556 + 914519864*x^555 + 458326840*x^554 + 846364356*x^553 + 1048948157*x^552 + 276890468*x^551 + 211463242*x^550 + 611009955*x^549 + 41350370*x^548 + 1120260432*x^547 + 1217213406*x^546 + 1096884636*x^545 + 107298827*x^544 + 556646889*x^543 + 514714957*x^542 + 592531623*x^541 + 1185635127*x^540 + 866796164*x^539 + 1199009440*x^538 + 760543377*x^537 + 135043128*x^536 + 1184521976*x^535 + 53368352*x^534 + 614063947*x^533 + 117184488*x^532 + 1090625549*x^531 + 928160285*x^530 + 1065640157*x^529 + 307397590*x^528 + 383318068*x^527 + 890835908*x^526 + 416986540*x^525 + 222852700*x^524 + 965323537*x^523 + 151764017*x^522 + 193722745*x^521 + 439803983*x^520 + 942882901*x^519 + 56286764*x^518 + 824204572*x^517 + 478793274*x^516 + 183238303*x^515 + 922253103*x^514 + 5444136*x^513 + 402856270*x^512 + 508652113*x^511 + 898341402*x^510 + 56743140*x^509 + 179078829*x^508 + 360574641*x^507 + 691533190*x^506 + 982373838*x^505 + 719429684*x^504 + 962339948*x^503 + 1097706834*x^502 + 682588935*x^501 + 1193566532*x^500 + 1140505780*x^499 + 1167874911*x^498 + 669408623*x^497 + 15348570*x^496 + 896129486*x^495 + 100671957*x^494 + 1015786650*x^493 + 605094306*x^492 + 704959137*x^491 + 503877361*x^490 + 546763047*x^489 + 281625173*x^488 + 874599768*x^487 + 187483443*x^486 + 791213383*x^485 + 670376251*x^484 + 484751013*x^483 + 519454749*x^482 + 898655062*x^481 + 1088862155*x^480 + 843442957*x^479 + 429341712*x^478 + 869408179*x^477 + 921648096*x^476 + 526019939*x^475 + 856290375*x^474 + 531710459*x^473 + 1135323038*x^472 + 222776023*x^471 + 223826994*x^470 + 782612384*x^469 + 208579370*x^468 + 809908930*x^467 + 802818642*x^466 + 1182584545*x^465 + 245518705*x^464 + 114792460*x^463 + 646248449*x^462 + 63969962*x^461 + 761908644*x^460 + 523665668*x^459 + 1131060959*x^458 + 507746193*x^457 + 215968166*x^456 + 186113215*x^455 + 1117740378*x^454 + 649175082*x^453 + 396834257*x^452 + 274002774*x^451 + 626055138*x^450 + 924423066*x^449 + 81357715*x^448 + 1042994674*x^447 + 380053163*x^446 + 687766657*x^445 + 414805559*x^444 + 1118153385*x^443 + 1196507975*x^442 + 223759358*x^441 + 808836890*x^440 + 558230978*x^439 + 470920831*x^438 + 313868031*x^437 + 696317665*x^436 + 38725962*x^435 + 722983488*x^434 + 982704221*x^433 + 931470025*x^432 + 658261117*x^431 + 1043739465*x^430 + 422603501*x^429 + 879856656*x^428 + 977082068*x^427 + 593021461*x^426 + 955543544*x^425 + 194004912*x^424 + 1057355064*x^423 + 1153279801*x^422 + 1104874965*x^421 + 1157109085*x^420 + 54358054*x^419 + 802241073*x^418 + 489376522*x^417 + 250441773*x^416 + 740903923*x^415 + 81493461*x^414 + 966046559*x^413 + 295086523*x^412 + 1192114766*x^411 + 1186654005*x^410 + 768853461*x^409 + 302013033*x^408 + 1127093874*x^407 + 401944628*x^406 + 463364841*x^405 + 277324527*x^404 + 357826211*x^403 + 302642912*x^402 + 785232813*x^401 + 1155455395*x^400 + 240939622*x^399 + 1090741169*x^398 + 941697407*x^397 + 1108935255*x^396 + 63027943*x^395 + 415750779*x^394 + 36046273*x^393 + 172429619*x^392 + 563533800*x^391 + 961503349*x^390 + 356454474*x^389 + 586712431*x^388 + 572728001*x^387 + 670855384*x^386 + 268877633*x^385 + 51139525*x^384 + 806328542*x^383 + 790061093*x^382 + 140256246*x^381 + 430118720*x^380 + 924612224*x^379 + 923573107*x^378 + 1124645882*x^377 + 1044890409*x^376 + 509180566*x^375 + 371227114*x^374 + 161843486*x^373 + 296514161*x^372 + 454272518*x^371 + 755779732*x^370 + 295567281*x^369 + 1063635155*x^368 + 46603670*x^367 + 112353112*x^366 + 571920305*x^365 + 484055586*x^364 + 148075787*x^363 + 700140701*x^362 + 922814151*x^361 + 198283677*x^360 + 806078101*x^359 + 1218701262*x^358 + 679274064*x^357 + 408382456*x^356 + 284971608*x^355 + 1072737570*x^354 + 999420946*x^353 + 704897365*x^352 + 1147239838*x^351 + 1148707218*x^350 + 119677974*x^349 + 139766009*x^348 + 289899118*x^347 + 3099746*x^346 + 478334394*x^345 + 671867092*x^344 + 1123276962*x^343 + 1053910974*x^342 + 776016929*x^341 + 408840884*x^340 + 702734268*x^339 + 101137143*x^338 + 157330682*x^337 + 608473559*x^336 + 355406102*x^335 + 1189624142*x^334 + 87874850*x^333 + 1097033743*x^332 + 984835279*x^331 + 133446104*x^330 + 990221835*x^329 + 34152703*x^328 + 902602955*x^327 + 564227604*x^326 + 378045277*x^325 + 330935315*x^324 + 300442927*x^323 + 504016276*x^322 + 592727454*x^321 + 1075766200*x^320 + 718996149*x^319 + 823573424*x^318 + 834215705*x^317 + 430497892*x^316 + 879722938*x^315 + 968236501*x^314 + 262764692*x^313 + 37503817*x^312 + 607855810*x^311 + 1173289902*x^310 + 906609932*x^309 + 11948749*x^308 + 948969610*x^307 + 1130417155*x^306 + 892108695*x^305 + 1040897188*x^304 + 174698274*x^303 + 85414336*x^302 + 758730292*x^301 + 615781943*x^300 + 1215130735*x^299 + 1168693743*x^298 + 1070287857*x^297 + 501559848*x^296 + 485147924*x^295 + 1218893131*x^294 + 923876087*x^293 + 565056561*x^292 + 282754375*x^291 + 794028720*x^290 + 288419549*x^289 + 688387454*x^288 + 40339086*x^287 + 659115548*x^286 + 614342861*x^285 + 391568544*x^284 + 464738754*x^283 + 28669498*x^282 + 1115640335*x^281 + 870635325*x^280 + 126237247*x^279 + 1111165998*x^278 + 205027579*x^277 + 911218811*x^276 + 208748481*x^275 + 725176545*x^274 + 765151044*x^273 + 939495648*x^272 + 550038893*x^271 + 905707993*x^270 + 267107699*x^269 + 477779883*x^268 + 251985659*x^267 + 754082836*x^266 + 159569451*x^265 + 781616103*x^264 + 1098961576*x^263 + 1139687026*x^262 + 473401848*x^261 + 623689501*x^260 + 1012676202*x^259 + 76777202*x^258 + 170602576*x^257 + 266093330*x^256 + 732274753*x^255 + 193219366*x^254 + 610602682*x^253 + 749761392*x^252 + 536911921*x^251 + 1052883954*x^250 + 1139729422*x^249 + 617278363*x^248 + 603450863*x^247 + 877968049*x^246 + 1078543204*x^245 + 441578327*x^244 + 821469144*x^243 + 1083268726*x^242 + 592074734*x^241 + 431251183*x^240 + 1151073027*x^239 + 596034003*x^238 + 507176703*x^237 + 638155464*x^236 + 820097610*x^235 + 69713965*x^234 + 111089281*x^233 + 403306683*x^232 + 417322569*x^231 + 510992488*x^230 + 406068742*x^229 + 487323397*x^228 + 1105866147*x^227 + 126043214*x^226 + 565379393*x^225 + 774566507*x^224 + 94477834*x^223 + 301787901*x^222 + 891557978*x^221 + 246179873*x^220 + 76065360*x^219 + 632831219*x^218 + 967852970*x^217 + 982932236*x^216 + 457056482*x^215 + 611696056*x^214 + 187879254*x^213 + 919970751*x^212 + 726626422*x^211 + 744906999*x^210 + 514152204*x^209 + 400846913*x^208 + 1057213516*x^207 + 458393393*x^206 + 39867352*x^205 + 482474421*x^204 + 1017159775*x^203 + 1127386440*x^202 + 186890818*x^201 + 297371952*x^200 + 827010510*x^199 + 457757189*x^198 + 120047360*x^197 + 403406161*x^196 + 561776540*x^195 + 269984973*x^194 + 1105865523*x^193 + 356682370*x^192 + 521018201*x^191 + 714326305*x^190 + 230112489*x^189 + 468954949*x^188 + 428412182*x^187 + 418097923*x^186 + 648421330*x^185 + 119412602*x^184 + 1029175202*x^183 + 961854350*x^182 + 359274957*x^181 + 918516748*x^180 + 393392054*x^179 + 998769881*x^178 + 713880369*x^177 + 23918875*x^176 + 19140072*x^175 + 296443203*x^174 + 1036511543*x^173 + 208417465*x^172 + 856221174*x^171 + 724608949*x^170 + 1148614286*x^169 + 605394185*x^168 + 1037184954*x^167 + 1149508482*x^166 + 748219008*x^165 + 762595570*x^164 + 240812860*x^163 + 221590855*x^162 + 921277317*x^161 + 666749995*x^160 + 270085731*x^159 + 719780654*x^158 + 1023109552*x^157 + 948736441*x^156 + 942460534*x^155 + 1190076672*x^154 + 298412436*x^153 + 146236637*x^152 + 136974417*x^151 + 247369427*x^150 + 1164600849*x^149 + 80725190*x^148 + 563971590*x^147 + 838975230*x^146 + 605884308*x^145 + 695738052*x^144 + 457993644*x^143 + 608089160*x^142 + 279768415*x^141 + 167776427*x^140 + 99830319*x^139 + 724761513*x^138 + 838344856*x^137 + 349705095*x^136 + 700591961*x^135 + 495192008*x^134 + 166834844*x^133 + 829383641*x^132 + 689577635*x^131 + 1063098370*x^130 + 1217658142*x^129 + 210005674*x^128 + 709445493*x^127 + 890260692*x^126 + 11818873*x^125 + 356866298*x^124 + 657354178*x^123 + 1083325742*x^122 + 256937537*x^121 + 832141251*x^120 + 738779202*x^119 + 531375449*x^118 + 570407521*x^117 + 253499493*x^116 + 936295735*x^115 + 840539077*x^114 + 1108243632*x^113 + 518037787*x^112 + 512681158*x^111 + 659791034*x^110 + 615039004*x^109 + 6475754*x^108 + 112655504*x^107 + 135513268*x^106 + 814830817*x^105 + 312451349*x^104 + 459204360*x^103 + 536270797*x^102 + 487599107*x^101 + 995873996*x^100 + 947176358*x^99 + 161110841*x^98 + 1215850742*x^97 + 828031021*x^96 + 393857015*x^95 + 483165571*x^94 + 1169422374*x^93 + 185485308*x^92 + 1113820447*x^91 + 1217012548*x^90 + 591690262*x^89 + 230984245*x^88 + 1183186281*x^87 + 984746087*x^86 + 321334226*x^85 + 356396152*x^84 + 812358214*x^83 + 652862462*x^82 + 1159946831*x^81 + 1185692555*x^80 + 1101691161*x^79 + 1162783803*x^78 + 592033894*x^77 + 545367197*x^76 + 441688164*x^75 + 169491076*x^74 + 181297517*x^73 + 590332818*x^72 + 814337101*x^71 + 1148316386*x^70 + 700258144*x^69 + 719201877*x^68 + 1160695934*x^67 + 1186868159*x^66 + 508542038*x^65 + 1113702100*x^64 + 921032142*x^63 + 758636144*x^62 + 890540800*x^61 + 136808203*x^60 + 74886413*x^59 + 156077420*x^58 + 925473910*x^57 + 111404286*x^56 + 355116767*x^55 + 468038980*x^54 + 89708844*x^53 + 878616521*x^52 + 1154657871*x^51 + 677831135*x^50 + 903468800*x^49 + 890557208*x^48 + 1035114476*x^47 + 198189399*x^46 + 864375452*x^45 + 1164916963*x^44 + 929627324*x^43 + 418711325*x^42 + 97430691*x^41 + 1172413774*x^40 + 760600756*x^39 + 943281805*x^38 + 53033182*x^37 + 123566782*x^36 + 665472336*x^35 + 521103310*x^34 + 892876972*x^33 + 169828417*x^32 + 315862403*x^31 + 973295601*x^30 + 1036868940*x^29 + 469235131*x^28 + 1097609240*x^27 + 446027303*x^26 + 356219098*x^25 + 480790123*x^24 + 94742566*x^23 + 691728720*x^22 + 922852954*x^21 + 21648854*x^20 + 903452116*x^19 + 1043050543*x^18 + 867501915*x^17 + 402312961*x^16 + 772349320*x^15 + 806410607*x^14 + 573402289*x^13 + 103888540*x^12 + 147927873*x^11 + 1005161156*x^10 + 988774771*x^9 + 682875980*x^8 + 54946232*x^7 + 717143945*x^6 + 323577100*x^5 + 803064428*x^4 + 598462622*x^3 + 1110253556*x^2 + 764371182*x + 634648371
b = 735531500*x^1023 + 684755229*x^1022 + 978579144*x^1021 + 560225565*x^1020 + 758090578*x^1019 + 367477932*x^1018 + 326779415*x^1017 + 26800946*x^1016 + 199017905*x^1015 + 1156874439*x^1014 + 673969262*x^1013 + 617169647*x^1012 + 462256026*x^1011 + 303059784*x^1010 + 663728970*x^1009 + 376865711*x^1008 + 830705685*x^1007 + 573964358*x^1006 + 1210202059*x^1005 + 269197755*x^1004 + 586236496*x^1003 + 621987820*x^1002 + 485567868*x^1001 + 305700227*x^1000 + 1052698462*x^999 + 86861550*x^998 + 44767901*x^997 + 410897986*x^996 + 212344404*x^995 + 336381747*x^994 + 398182335*x^993 + 660275371*x^992 + 52728322*x^991 + 1193103469*x^990 + 684295535*x^989 + 1029981794*x^988 + 1051866415*x^987 + 418681909*x^986 + 976794520*x^985 + 1180496804*x^984 + 438513041*x^983 + 822843942*x^982 + 1119264881*x^981 + 790873853*x^980 + 1146506838*x^979 + 27016797*x^978 + 1149126201*x^977 + 967895459*x^976 + 1201841165*x^975 + 264216641*x^974 + 751855165*x^973 + 277480010*x^972 + 955969328*x^971 + 784721168*x^970 + 696371212*x^969 + 401164998*x^968 + 654719011*x^967 + 785183205*x^966 + 79070435*x^965 + 1140562925*x^964 + 1025154340*x^963 + 1044315421*x^962 + 392734282*x^961 + 234286141*x^960 + 962551866*x^959 + 133742245*x^958 + 998056106*x^957 + 781318236*x^956 + 23528574*x^955 + 1214036424*x^954 + 296666931*x^953 + 1211729921*x^952 + 561550286*x^951 + 634392845*x^950 + 422332555*x^949 + 765556851*x^948 + 1151849524*x^947 + 305981530*x^946 + 246290056*x^945 + 24304550*x^944 + 477073522*x^943 + 416104453*x^942 + 898162013*x^941 + 611609496*x^940 + 445765799*x^939 + 430180169*x^938 + 1151421310*x^937 + 439515367*x^936 + 795257572*x^935 + 578106992*x^934 + 929259980*x^933 + 550407102*x^932 + 1219047347*x^931 + 15972593*x^930 + 515513177*x^929 + 679675449*x^928 + 914537835*x^927 + 156230965*x^926 + 385558312*x^925 + 1036365654*x^924 + 1098274877*x^923 + 348628203*x^922 + 1093802915*x^921 + 1162728002*x^920 + 200502246*x^919 + 551049082*x^918 + 969116717*x^917 + 1127382445*x^916 + 968172543*x^915 + 346881523*x^914 + 41744706*x^913 + 335042561*x^912 + 593895276*x^911 + 15888292*x^910 + 324866127*x^909 + 937351605*x^908 + 347255852*x^907 + 1120419679*x^906 + 249832197*x^905 + 896923860*x^904 + 129801128*x^903 + 207849052*x^902 + 386825059*x^901 + 823406098*x^900 + 977635408*x^899 + 108813100*x^898 + 561865827*x^897 + 718000532*x^896 + 48090035*x^895 + 832337939*x^894 + 1084389292*x^893 + 793335438*x^892 + 1095245016*x^891 + 1080787282*x^890 + 122666287*x^889 + 937313249*x^888 + 62818846*x^887 + 1170462486*x^886 + 182439366*x^885 + 792906343*x^884 + 1205386767*x^883 + 310389549*x^882 + 603676058*x^881 + 671251954*x^880 + 640345010*x^879 + 1087374504*x^878 + 119769446*x^877 + 135989573*x^876 + 880703983*x^875 + 613578242*x^874 + 1207874966*x^873 + 972002390*x^872 + 644470053*x^871 + 335762119*x^870 + 1079917808*x^869 + 1023711373*x^868 + 861485470*x^867 + 230979333*x^866 + 683284149*x^865 + 645804102*x^864 + 577971621*x^863 + 33779989*x^862 + 915467237*x^861 + 834966216*x^860 + 445758874*x^859 + 685228217*x^858 + 979609284*x^857 + 842509205*x^856 + 221373358*x^855 + 150166201*x^854 + 927937340*x^853 + 995054125*x^852 + 704623324*x^851 + 1112892592*x^850 + 782816865*x^849 + 878518510*x^848 + 391872241*x^847 + 30062686*x^846 + 108900016*x^845 + 1034780269*x^844 + 1190084541*x^843 + 441686497*x^842 + 117953957*x^841 + 840802549*x^840 + 903238790*x^839 + 551715093*x^838 + 539420097*x^837 + 1007110444*x^836 + 673864283*x^835 + 756402005*x^834 + 197892310*x^833 + 981720851*x^832 + 798897509*x^831 + 1127242378*x^830 + 666754217*x^829 + 685248618*x^828 + 327773092*x^827 + 390697118*x^826 + 912223373*x^825 + 482947333*x^824 + 1110169857*x^823 + 780612147*x^822 + 194698743*x^821 + 716386043*x^820 + 424946693*x^819 + 22701975*x^818 + 293011366*x^817 + 947695756*x^816 + 1188483932*x^815 + 1002073886*x^814 + 1078210750*x^813 + 1127684166*x^812 + 719332394*x^811 + 1072532713*x^810 + 550629553*x^809 + 188195613*x^808 + 614412704*x^807 + 649960359*x^806 + 1010011298*x^805 + 824975518*x^804 + 311757403*x^803 + 93674481*x^802 + 380323800*x^801 + 1086623904*x^800 + 240170088*x^799 + 956396081*x^798 + 939969890*x^797 + 131843464*x^796 + 1045744996*x^795 + 424359277*x^794 + 550616456*x^793 + 1061637035*x^792 + 444548551*x^791 + 677546521*x^790 + 149605032*x^789 + 829567560*x^788 + 516053142*x^787 + 1191529914*x^786 + 294270928*x^785 + 142024389*x^784 + 584911191*x^783 + 307856659*x^782 + 81514660*x^781 + 543784156*x^780 + 108008163*x^779 + 13154295*x^778 + 155266054*x^777 + 663702892*x^776 + 782494602*x^775 + 747547833*x^774 + 242456376*x^773 + 669844220*x^772 + 552894098*x^771 + 1036366706*x^770 + 1074841665*x^769 + 720745418*x^768 + 1137936670*x^767 + 840875363*x^766 + 476498840*x^765 + 1088669461*x^764 + 1249649*x^763 + 882277578*x^762 + 37842126*x^761 + 398977801*x^760 + 328296234*x^759 + 536342859*x^758 + 608139240*x^757 + 897424944*x^756 + 76562916*x^755 + 428081420*x^754 + 627420927*x^753 + 265131678*x^752 + 1034443577*x^751 + 177902661*x^750 + 490977141*x^749 + 1084536775*x^748 + 1189221123*x^747 + 854191429*x^746 + 952038058*x^745 + 891288300*x^744 + 929356576*x^743 + 223874272*x^742 + 220297702*x^741 + 1099283305*x^740 + 1008574448*x^739 + 619949004*x^738 + 747199791*x^737 + 760703880*x^736 + 7682727*x^735 + 88566484*x^734 + 733742620*x^733 + 381443925*x^732 + 799269923*x^731 + 233342676*x^730 + 1205696983*x^729 + 765306727*x^728 + 29342855*x^727 + 287728251*x^726 + 214358216*x^725 + 355991367*x^724 + 344973841*x^723 + 436344093*x^722 + 547944829*x^721 + 1041405031*x^720 + 368771692*x^719 + 37426577*x^718 + 502936636*x^717 + 732825913*x^716 + 518778589*x^715 + 561797784*x^714 + 773068766*x^713 + 75615306*x^712 + 668933267*x^711 + 628975723*x^710 + 1140697439*x^709 + 108807342*x^708 + 283945737*x^707 + 701674528*x^706 + 1120373548*x^705 + 421627231*x^704 + 260846853*x^703 + 292537012*x^702 + 583513440*x^701 + 609720259*x^700 + 831373721*x^699 + 1126099385*x^698 + 431095431*x^697 + 296863241*x^696 + 371013827*x^695 + 549980853*x^694 + 550174635*x^693 + 620963563*x^692 + 952040422*x^691 + 1150044500*x^690 + 893175261*x^689 + 1139857784*x^688 + 972717568*x^687 + 735672517*x^686 + 1177501026*x^685 + 765934764*x^684 + 710762091*x^683 + 871268519*x^682 + 969318271*x^681 + 286261161*x^680 + 65128931*x^679 + 1100922672*x^678 + 47619662*x^677 + 981578224*x^676 + 67232154*x^675 + 1928142*x^674 + 817643007*x^673 + 675713298*x^672 + 185236805*x^671 + 331446457*x^670 + 129023118*x^669 + 431426370*x^668 + 1154277684*x^667 + 723182950*x^666 + 1144823093*x^665 + 822001162*x^664 + 356099532*x^663 + 705989193*x^662 + 878712048*x^661 + 1095044481*x^660 + 332193401*x^659 + 613329359*x^658 + 673744151*x^657 + 808080280*x^656 + 225562949*x^655 + 185686220*x^654 + 742469973*x^653 + 986152315*x^652 + 13611550*x^651 + 535747170*x^650 + 233786507*x^649 + 27955348*x^648 + 1004446959*x^647 + 1071164149*x^646 + 265258708*x^645 + 63221383*x^644 + 682228580*x^643 + 867131152*x^642 + 997600620*x^641 + 993922001*x^640 + 693252545*x^639 + 865655581*x^638 + 518295141*x^637 + 902072633*x^636 + 704953646*x^635 + 587251157*x^634 + 99168972*x^633 + 1105480730*x^632 + 1040404159*x^631 + 436113220*x^630 + 152714904*x^629 + 697469981*x^628 + 1185372838*x^627 + 216027999*x^626 + 616083931*x^625 + 399419685*x^624 + 23193568*x^623 + 1174129641*x^622 + 75724376*x^621 + 570399858*x^620 + 754947446*x^619 + 1037864447*x^618 + 794730343*x^617 + 60369472*x^616 + 750769016*x^615 + 61444481*x^614 + 333194445*x^613 + 1109236037*x^612 + 513379869*x^611 + 706807998*x^610 + 999669914*x^609 + 1198194959*x^608 + 336044172*x^607 + 402719207*x^606 + 1050007981*x^605 + 429464593*x^604 + 679293134*x^603 + 734513317*x^602 + 838385265*x^601 + 990800608*x^600 + 1162093896*x^599 + 173467508*x^598 + 123947890*x^597 + 325712596*x^596 + 1049522320*x^595 + 1072653958*x^594 + 565759817*x^593 + 549918485*x^592 + 574268523*x^591 + 1052593520*x^590 + 474323970*x^589 + 262787725*x^588 + 1091470590*x^587 + 782664905*x^586 + 1201833996*x^585 + 808712564*x^584 + 619522329*x^583 + 233329446*x^582 + 730502283*x^581 + 1017501853*x^580 + 306080194*x^579 + 283641594*x^578 + 195324593*x^577 + 1116741123*x^576 + 289439631*x^575 + 206064600*x^574 + 280021778*x^573 + 425409216*x^572 + 1107952582*x^571 + 131800177*x^570 + 106903346*x^569 + 72306234*x^568 + 934072451*x^567 + 242740893*x^566 + 106611451*x^565 + 429378634*x^564 + 127624569*x^563 + 587315789*x^562 + 932709753*x^561 + 523886142*x^560 + 110330665*x^559 + 963244036*x^558 + 227339325*x^557 + 185882207*x^556 + 987833442*x^555 + 981380006*x^554 + 1140813804*x^553 + 538704418*x^552 + 842520362*x^551 + 597627400*x^550 + 165232274*x^549 + 900076209*x^548 + 311342603*x^547 + 477271753*x^546 + 1072907066*x^545 + 1066126181*x^544 + 791702251*x^543 + 623246063*x^542 + 1082681410*x^541 + 759396967*x^540 + 878108937*x^539 + 724607060*x^538 + 79223685*x^537 + 307312027*x^536 + 234246571*x^535 + 330319932*x^534 + 274254378*x^533 + 1082820468*x^532 + 68920838*x^531 + 1195376541*x^530 + 170971307*x^529 + 399525324*x^528 + 238798853*x^527 + 664426862*x^526 + 269949285*x^525 + 698202786*x^524 + 88964561*x^523 + 635539315*x^522 + 1016514687*x^521 + 122364467*x^520 + 1095096646*x^519 + 513834099*x^518 + 672478524*x^517 + 47526709*x^516 + 48782616*x^515 + 166225959*x^514 + 810099682*x^513 + 168540411*x^512 + 30055377*x^511 + 817325819*x^510 + 202717189*x^509 + 739906349*x^508 + 186072589*x^507 + 451966755*x^506 + 684027658*x^505 + 251331059*x^504 + 591972494*x^503 + 289197098*x^502 + 829928406*x^501 + 160528626*x^500 + 90951219*x^499 + 496118642*x^498 + 117818178*x^497 + 215417436*x^496 + 937904122*x^495 + 962080493*x^494 + 423647737*x^493 + 1094089608*x^492 + 97559711*x^491 + 412409151*x^490 + 1039695658*x^489 + 461079746*x^488 + 564664118*x^487 + 2231630*x^486 + 667569567*x^485 + 471400483*x^484 + 691739455*x^483 + 146641223*x^482 + 445509678*x^481 + 788647561*x^480 + 100316571*x^479 + 927803124*x^478 + 225739054*x^477 + 339283562*x^476 + 741552554*x^475 + 674303545*x^474 + 610706793*x^473 + 1045437706*x^472 + 758427998*x^471 + 518677374*x^470 + 1020530386*x^469 + 81672436*x^468 + 684553666*x^467 + 36416557*x^466 + 1083076029*x^465 + 63903696*x^464 + 655765095*x^463 + 464055997*x^462 + 874368360*x^461 + 909538282*x^460 + 1084815716*x^459 + 971305398*x^458 + 504958756*x^457 + 941782746*x^456 + 410981017*x^455 + 44463213*x^454 + 57796260*x^453 + 633624768*x^452 + 902476625*x^451 + 1190884714*x^450 + 30960289*x^449 + 698111360*x^448 + 507015564*x^447 + 595305556*x^446 + 1170147546*x^445 + 595449153*x^444 + 1132050715*x^443 + 566093951*x^442 + 1125890381*x^441 + 864044563*x^440 + 608408253*x^439 + 128031905*x^438 + 951152598*x^437 + 41054884*x^436 + 1012755213*x^435 + 1091670374*x^434 + 481898210*x^433 + 1007980179*x^432 + 43301236*x^431 + 6478999*x^430 + 1175215424*x^429 + 597862715*x^428 + 441537430*x^427 + 339705054*x^426 + 289227345*x^425 + 795113772*x^424 + 404870950*x^423 + 997272819*x^422 + 634256255*x^421 + 453060086*x^420 + 821493547*x^419 + 842289852*x^418 + 223251279*x^417 + 929721613*x^416 + 63980045*x^415 + 298369623*x^414 + 1026287144*x^413 + 979092254*x^412 + 1182904024*x^411 + 298048453*x^410 + 653297794*x^409 + 365769179*x^408 + 45373617*x^407 + 7228243*x^406 + 1086374067*x^405 + 389455721*x^404 + 992518297*x^403 + 433929335*x^402 + 1149626197*x^401 + 90006250*x^400 + 1011632630*x^399 + 940906615*x^398 + 564772117*x^397 + 692974220*x^396 + 561321375*x^395 + 1095715303*x^394 + 1006114558*x^393 + 95516055*x^392 + 640816811*x^391 + 869737844*x^390 + 248741996*x^389 + 101754352*x^388 + 253268107*x^387 + 593472036*x^386 + 627778298*x^385 + 801877646*x^384 + 286581226*x^383 + 645931883*x^382 + 373119745*x^381 + 461109006*x^380 + 594214135*x^379 + 751634451*x^378 + 706229440*x^377 + 247985412*x^376 + 993987710*x^375 + 618989435*x^374 + 600506682*x^373 + 179955505*x^372 + 956234357*x^371 + 1049030902*x^370 + 727597507*x^369 + 1196607714*x^368 + 610634244*x^367 + 619865634*x^366 + 849131167*x^365 + 1094185730*x^364 + 685353152*x^363 + 299082549*x^362 + 1076769237*x^361 + 792938001*x^360 + 885082721*x^359 + 1198739364*x^358 + 273154602*x^357 + 597517874*x^356 + 351418158*x^355 + 621945565*x^354 + 949756104*x^353 + 1020290901*x^352 + 315372660*x^351 + 291246927*x^350 + 1016861207*x^349 + 171467993*x^348 + 1074074496*x^347 + 660775696*x^346 + 562891589*x^345 + 258618000*x^344 + 521058831*x^343 + 152819838*x^342 + 1141330990*x^341 + 383408903*x^340 + 677850803*x^339 + 165908062*x^338 + 66975904*x^337 + 510786934*x^336 + 32306220*x^335 + 708115806*x^334 + 474352780*x^333 + 963188335*x^332 + 151844162*x^331 + 907339624*x^330 + 456166118*x^329 + 111742252*x^328 + 318018829*x^327 + 624012970*x^326 + 255354390*x^325 + 1218329311*x^324 + 375000855*x^323 + 54956044*x^322 + 13543809*x^321 + 671163260*x^320 + 226676913*x^319 + 1193470867*x^318 + 477161216*x^317 + 519506783*x^316 + 748987057*x^315 + 768531367*x^314 + 327816599*x^313 + 59056092*x^312 + 520958252*x^311 + 243337260*x^310 + 608632530*x^309 + 65258636*x^308 + 1012579720*x^307 + 400176357*x^306 + 104583966*x^305 + 1114827176*x^304 + 70705682*x^303 + 5320656*x^302 + 1207465008*x^301 + 1211372826*x^300 + 886104873*x^299 + 747144635*x^298 + 227753814*x^297 + 427912588*x^296 + 425232985*x^295 + 135219277*x^294 + 541439233*x^293 + 82586191*x^292 + 1024575564*x^291 + 408418547*x^290 + 1076407665*x^289 + 184646604*x^288 + 894569780*x^287 + 730742386*x^286 + 473643018*x^285 + 561906151*x^284 + 582231889*x^283 + 928617667*x^282 + 460594931*x^281 + 946340582*x^280 + 881007408*x^279 + 655553538*x^278 + 107738502*x^277 + 958107338*x^276 + 874269820*x^275 + 689734430*x^274 + 1025286771*x^273 + 809509338*x^272 + 126580761*x^271 + 425724981*x^270 + 91398446*x^269 + 915486182*x^268 + 750598785*x^267 + 331692120*x^266 + 266239686*x^265 + 41813860*x^264 + 1003196915*x^263 + 1006275694*x^262 + 958171508*x^261 + 387655573*x^260 + 529686749*x^259 + 2533683*x^258 + 851532040*x^257 + 515865631*x^256 + 331149910*x^255 + 1058283457*x^254 + 478391568*x^253 + 1020601120*x^252 + 193954604*x^251 + 125558467*x^250 + 916367669*x^249 + 965664721*x^248 + 737411958*x^247 + 145954639*x^246 + 787702411*x^245 + 256023548*x^244 + 831752864*x^243 + 637799028*x^242 + 202325459*x^241 + 189858829*x^240 + 221236168*x^239 + 276967229*x^238 + 732958371*x^237 + 31622618*x^236 + 558911372*x^235 + 257580689*x^234 + 490167674*x^233 + 1164269554*x^232 + 765931664*x^231 + 89716985*x^230 + 639008878*x^229 + 716033538*x^228 + 186948569*x^227 + 870251868*x^226 + 383121640*x^225 + 604362204*x^224 + 405526662*x^223 + 127371887*x^222 + 543669202*x^221 + 823112915*x^220 + 523517382*x^219 + 791437322*x^218 + 1069279817*x^217 + 960628355*x^216 + 1012582276*x^215 + 1200088601*x^214 + 927011022*x^213 + 830570829*x^212 + 700668365*x^211 + 1205573850*x^210 + 276778781*x^209 + 786305215*x^208 + 928215922*x^207 + 154393796*x^206 + 169298902*x^205 + 177646296*x^204 + 173339370*x^203 + 287217637*x^202 + 1077403939*x^201 + 1004965535*x^200 + 677352462*x^199 + 545192340*x^198 + 464170452*x^197 + 381853900*x^196 + 205643848*x^195 + 973330672*x^194 + 1148733662*x^193 + 458436519*x^192 + 68604889*x^191 + 193530886*x^190 + 141661386*x^189 + 1117183144*x^188 + 153035244*x^187 + 830892599*x^186 + 795500906*x^185 + 67041425*x^184 + 617209634*x^183 + 180547177*x^182 + 1183445159*x^181 + 303603618*x^180 + 842724764*x^179 + 784982658*x^178 + 1199356684*x^177 + 321497016*x^176 + 513738925*x^175 + 465949450*x^174 + 981246204*x^173 + 814398377*x^172 + 950247970*x^171 + 720838080*x^170 + 399493165*x^169 + 735365971*x^168 + 109745845*x^167 + 897998838*x^166 + 547497972*x^165 + 174675208*x^164 + 716115074*x^163 + 237209800*x^162 + 186394653*x^161 + 876995839*x^160 + 1187252196*x^159 + 819282320*x^158 + 44596523*x^157 + 679033559*x^156 + 736746236*x^155 + 1184916922*x^154 + 451294643*x^153 + 443590366*x^152 + 304384335*x^151 + 1064695584*x^150 + 602535518*x^149 + 684486124*x^148 + 863476315*x^147 + 496170722*x^146 + 737062216*x^145 + 285799611*x^144 + 1085153158*x^143 + 247783563*x^142 + 1208043659*x^141 + 208776666*x^140 + 117730360*x^139 + 279620264*x^138 + 273045622*x^137 + 893971194*x^136 + 240743423*x^135 + 1143029271*x^134 + 326725356*x^133 + 294174585*x^132 + 672819095*x^131 + 138843366*x^130 + 1176670148*x^129 + 573825049*x^128 + 835249905*x^127 + 778468469*x^126 + 300257393*x^125 + 409352854*x^124 + 953527813*x^123 + 653640743*x^122 + 1210615840*x^121 + 596684403*x^120 + 46012813*x^119 + 510765516*x^118 + 1213476223*x^117 + 1132779740*x^116 + 769195645*x^115 + 963749389*x^114 + 843804183*x^113 + 109759209*x^112 + 493130294*x^111 + 1122857844*x^110 + 1130618881*x^109 + 648465049*x^108 + 364595574*x^107 + 410134064*x^106 + 597836905*x^105 + 831243271*x^104 + 226275998*x^103 + 686704033*x^102 + 662011231*x^101 + 112226051*x^100 + 623946037*x^99 + 469742204*x^98 + 369854172*x^97 + 731154062*x^96 + 352916654*x^95 + 45991298*x^94 + 614913911*x^93 + 632337602*x^92 + 327529986*x^91 + 111251878*x^90 + 657089210*x^89 + 499853920*x^88 + 966818975*x^87 + 454584975*x^86 + 116582431*x^85 + 619242494*x^84 + 455382561*x^83 + 246350547*x^82 + 495191129*x^81 + 900852972*x^80 + 264825752*x^79 + 426813960*x^78 + 478124215*x^77 + 1080567657*x^76 + 858353771*x^75 + 215115660*x^74 + 963682245*x^73 + 964445096*x^72 + 73603206*x^71 + 734630202*x^70 + 199652522*x^69 + 520021635*x^68 + 763256200*x^67 + 861482624*x^66 + 890485659*x^65 + 523362913*x^64 + 785087110*x^63 + 381314881*x^62 + 843850504*x^61 + 61951613*x^60 + 119100925*x^59 + 531827488*x^58 + 199818669*x^57 + 592207491*x^56 + 354682041*x^55 + 1015447358*x^54 + 328324806*x^53 + 24880841*x^52 + 516663598*x^51 + 716706066*x^50 + 1042483154*x^49 + 331433641*x^48 + 929901382*x^47 + 502140671*x^46 + 48123362*x^45 + 1112586174*x^44 + 14618102*x^43 + 764832169*x^42 + 446768463*x^41 + 920421919*x^40 + 491851586*x^39 + 24718814*x^38 + 83091454*x^37 + 155770396*x^36 + 12824441*x^35 + 954371888*x^34 + 318592841*x^33 + 788251579*x^32 + 246435934*x^31 + 387083299*x^30 + 395226231*x^29 + 646811732*x^28 + 1131418388*x^27 + 1135116504*x^26 + 986902782*x^25 + 323457413*x^24 + 521885110*x^23 + 234655676*x^22 + 965166497*x^21 + 755967054*x^20 + 574743395*x^19 + 1175664410*x^18 + 117322371*x^17 + 794664856*x^16 + 570463*x^15 + 1148572518*x^14 + 439320220*x^13 + 815953366*x^12 + 389050726*x^11 + 1167287391*x^10 + 397052468*x^9 + 275572458*x^8 + 548665509*x^7 + 1202175986*x^6 + 518662014*x^5 + 1084425257*x^4 + 7854568*x^3 + 274607457*x^2 + 162444786*x + 410560230

ps = [x - 1,x + 1,x^2 + 1,x^4 + 1,x^8 + 1,x^16 + 1,x^32 + 1,x^64 + 1]

def flatter(M):
    # compile https://github.com/keeganryan/flatter and put it in $PATH
    z = "[[" + "]\n[".join(" ".join(map(str, row)) for row in M) + "]]"
    ret = check_output(["flatter"], input=z.encode())
    return matrix(M.nrows(), M.ncols(), map(int, findall(b"-?\\d+", ret)))

def solve(poly, a, b, slen=None):
    # solve for a*s+e=b (mod poly)
    # where s and e are small
    # and len(s) = slen
    global mat, mat2
    n = poly.degree()
    if slen is None:
        slen = n
    print(f"Try solving with deg(poly) = {n}")
    t0 = time()
    main_block = matrix([vector(a * x**i % poly) for i in range(n)])
    approx = 512 // n  # approximation for the average of target vector
    mat = block_matrix(
        ZZ,
        [
            [1, -main_block, 0],
            [0, q, 0],
            # kannan embedding
            [
                0,
                matrix(vector(b % poly)),
                matrix([[approx]]),
            ],
        ],
    )
    mat[:, slen:n] *= q  # force zero
    print(f"Lattice size = {mat.dimensions()}")
    mat2 = flatter(mat)
    print(f"{mat.nrows()}x{mat.ncols()} lattice reduced in {time()-t0}")
    for ret in mat2:
        if ret[-1] < 0:
            ret = -ret
        if ret[-1] == approx:
            print(ret)
            print()
            return F(list(ret[:n]))

rs = [solve(p, a, b) for p in ps]
L = lcm(ps[:-1])  # deg(L) = 256
s_mod_L = crt(rs, ps)  # this is s (mod L)
e_mod_L = (b - a * s_mod_L) % L
print('---------------')
print(s_mod_L)
print(e_mod_L)



q = 1219077173
P.<x> = PolynomialRing(Zmod(q))
A = 114*x^63 + 49*x^62 + 104*x^61 + 56*x^60 + 84*x^59 + 49*x^58 + 60*x^57 + 37*x^56 + 36*x^55 + 55*x^54 + 106*x^53 + 40*x^52 + 111*x^51 + 61*x^50 + 111*x^49 + 68*x^48 + 111*x^47 + 125*x^46 + 81*x^45 + 68*x^44 + 35*x^43 + 53*x^42 + 94*x^41 + 62*x^40 + 74*x^39 + 60*x^38 + 33*x^37 + 111*x^36 + 67*x^35 + 64*x^34 + 75*x^33 + 65*x^32 + 33*x^31 + 121*x^30 + 108*x^29 + 111*x^28 + 80*x^27 + 95*x^26 + 99*x^25 + 49*x^24 + 109*x^23 + 111*x^22 + 116*x^21 + 79*x^20 + 108*x^19 + 99*x^18 + 121*x^17 + 67*x^16 + 95*x^15 + 119*x^14 + 48*x^13 + 110*x^12 + 75*x^11 + 95*x^10 + 89*x^9 + 49*x^8 + 49*x^7 + 52*x^6 + 64*x^5 + 82*x^4 + 95*x^3 + 117*x^2 + 48*x + 89
AA = A.coefficient()
flag = ''
for i in range(len(AA)):
    flag += chr(AA[i])
print(flag)

SPN

中间相遇攻击，round_func是线性的，可以反推，正向跑两轮需要知道key的前20bit，由于enc中的

for i in range(16):

Y[i] ^= K[kstart+i]

函数，逆向跑两轮需要key的后24bit，先跑出正向两轮的所有结果，再跑逆向两轮，如果与正向相同，则输出。

from hashlib import sha256
from Crypto.Util.number import long_to_bytes
from tqdm import tqdm

def bin_to_list(r, bit_len):
    list = [r >> d & 1 for d in range(bit_len)][::-1]
    return list

def list_to_int(list):
    return int("".join(str(i) for i in list), 2)

Pbox=[1, 5, 9, 13, 2, 6, 10, 14, 3, 7, 11, 15, 4, 8, 12, 16]
Sbox=[14, 13, 11, 0, 2, 1, 4, 15, 7, 10, 8, 5, 9, 12, 3, 6]

def round_func(X,r,K):
    kstart=4*r - 4
    XX = [0] * 16
    for i in range(16):
        XX[i] = X[i] ^ K[kstart+i]
    for i in range(4):
        value = list_to_int(XX[4*i:4*i+4])
        s_value = Sbox[value]
        s_list = bin_to_list(s_value, 4)
        XX[4*i],XX[4*i+1],XX[4*i+2],XX[4*i+3] = s_list[0],s_list[1],s_list[2],s_list[3]

    Y=[0] * 16
    for i in range(16):
        Y[Pbox[i]-1]=XX[i]
    return Y

def enc(X,K):
    Y = round_func(X,1,K)
    Y = round_func(Y,2,K)
    # Y = round_func(Y,3,K)
    # Y = round_func(Y,4,K)
    #
    # kstart=4*5 - 4
    # for i in range(16):
    #     Y[i] ^= K[kstart+i]
    return Y

def re_round_func(Y,r,K):
    XX = [0]*16
    for i in range(16):
        XX[i] = Y[Pbox[i]-1]
    for i in range(4):
        value = list_to_int(XX[4 * i:4 * i + 4])
        s_value = Sbox.index(value)
        s_list = bin_to_list(s_value, 4)
        XX[4 * i], XX[4 * i + 1], XX[4 * i + 2], XX[4 * i + 3] = s_list[0], s_list[1], s_list[2], s_list[3]
    kstart = 4 * r - 4
    X = [0] * 16
    for i in range(16):
        X[i] = XX[i] ^ K[kstart+i]
    return X

x1,x2,x3,x4 = [0]*16,[0]*16,[0]*16,[0]*16
x1[0],x2[4],x3[8],x4[12] = 1,1,1,1
forward = set()
for i in tqdm(range(2**20)):
    K0 = bin_to_list(i,20)
    CC1,CC2,CC3,CC4 = enc(x1,K0),enc(x2,K0),enc(x3,K0),enc(x4,K0)
    num = list_to_int(CC1+CC2+CC3+CC4)
    forward.add(num)

C_final0 = [0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1]
C_final1 = [0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0]
C_final2 = [0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1]
C_final3 = [0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1]

for i in tqdm(range(2**24)):
    K1 = bin_to_list(i,24)
    c_final0,c_final1,c_final2,c_final3 = [0]*16,[0]*16,[0]*16,[0]*16
    for i0 in range(16):
        c_final0[i0] = K1[8+i0]^C_final0[i0]
        c_final1[i0] = K1[8+i0]^C_final1[i0]
        c_final2[i0] = K1[8+i0]^C_final2[i0]
        c_final3[i0] = K1[8+i0]^C_final3[i0]
    C1,C2,C3,C4 = re_round_func(c_final0,2,K1),re_round_func(c_final1,2,K1),re_round_func(c_final2,2,K1),re_round_func(c_final3,2,K1)
    C1,C2,C3,C4 = re_round_func(C1,1,K1),re_round_func(C2,1,K1),re_round_func(C3,1,K1),re_round_func(C4,1,K1)
    num1 = list_to_int(C1+C2+C3+C4)
    if num1 in forward:
        print(K1)
        break

得到后24bit的key，前八bit正向加密爆破。

from hashlib import sha256
from Crypto.Util.number import long_to_bytes
from tqdm import tqdm

def bin_to_list(r, bit_len):
    list = [r >> d & 1 for d in range(bit_len)][::-1]
    return list

def list_to_int(list):
    return int("".join(str(i) for i in list), 2)

Pbox=[1, 5, 9, 13, 2, 6, 10, 14, 3, 7, 11, 15, 4, 8, 12, 16]
Sbox=[14, 13, 11, 0, 2, 1, 4, 15, 7, 10, 8, 5, 9, 12, 3, 6]

def round_func(X,r,K):
    kstart=4*r - 4
    XX = [0] * 16
    for i in range(16):
        XX[i] = X[i] ^ K[kstart+i]
    for i in range(4):
        value = list_to_int(XX[4*i:4*i+4])
        s_value = Sbox[value]
        s_list = bin_to_list(s_value, 4)
        XX[4*i],XX[4*i+1],XX[4*i+2],XX[4*i+3] = s_list[0],s_list[1],s_list[2],s_list[3]

    Y=[0] * 16
    for i in range(16):
        Y[Pbox[i]-1]=XX[i]
    return Y

def enc(X,K):
    Y = round_func(X,1,K)
    Y = round_func(Y,2,K)
    Y = round_func(Y,3,K)
    Y = round_func(Y,4,K)

    kstart=4*5 - 4
    for i in range(16):
        Y[i] ^= K[kstart+i]
    return Y
x1,x2,x3,x4 = [0]*16,[0]*16,[0]*16,[0]*16
x1[0],x2[4],x3[8],x4[12] = 1,1,1,1

k = [1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0]
for i in range(2**8):
    key = bin_to_list(i,8) + k
    C1,C2,C3,C4 = enc(x1,key),enc(x2,key),enc(x3,key),enc(x4,key)
    if C1 ==  [0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1] and C2 == [0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0]:
        print(key)
        hash_value = sha256(long_to_bytes(list_to_int(key))).hexdigest()
        print(hash_value)

MDH

基于矩阵群的 DH 密钥交换，只要能求解矩阵离散对数，这题就迎刃而解了。可以参考 The Discrete Logarithm Problem in Matrix Groups 以及 The Discrete Logarithm Problem in GL(n, q) 两篇文献。它们详细阐述了如何基于若尔当标准型分解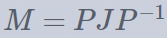将矩阵离散对数问题转换为有限域上的离散对数问题。

本题矩阵未定义在有限域上，而是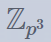上，并且矩阵不可逆，部分特征值未定义在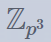，这就导致了这题不能直接用若尔当标准型来做。了解若尔当标准型中的数学内核，这题可以直接从矩阵特征多项式的根来做。给定矩阵，其特征多项式的本质就是：

从定义不难得到：特征多项式的根就是矩阵的特征值，而根据若尔当标准型在扩域上的分解形式，矩阵特征值会保持幂同态，即 M的一个特征值λ，在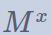中对应的特征值就是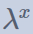，。因此我们同样可以把矩阵离散对数降级到它元素有限域上的离散对数问题。而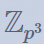上的离散对数在本题的场景下是简单的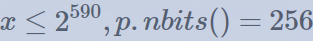（），详细请参考另外两篇博客：

矩阵离散对数规约问题可以参考博客基于特征值的矩阵 DLP。
整数环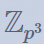上的离散对数问题可以参考博客 Discrete-Logarithm-Over-Z-p-r。

EXP：

from hashlib import sha256
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from output import p, M, Ma, Mb, ct
p = 79008119711208495443423312926395331665944721527891616265679009115440018598629
Gp3 = Zmod(p^3)
M = matrix(Gp3, M)
t = randint(1, 2^560)
Mt = M^t
Ma = matrix(Gp3, Ma)
Mb = matrix(Gp3, Mb)

print(t)
print(f"f[x] := {M.charpoly()};")
print(f"g[x] := {Ma.charpoly()};")
print(f"h[x] := {Mb.charpoly()};")
print(f"ft[x] := {Mt.charpoly()};")

def binomial_dlog_sub(y,g,p,q,r=2):
    C = ZZ(pow(y, q, p^r))
    B = ZZ(pow(g, q, p^r))
    kx = (C - 1)//p^(r-1)
    k =  (B - 1)//p^(r-1)
    x = ZZ(kx * pow(k, -1, p) % p)
    return x

def binomial_dlog(y,g,p,q,r):
    # solve y = g^x \mod p^r where q=phi(p) such that g^q = 1 \mod p
    assert r >= 2
    y = ZZ(y)
    g = ZZ(g)
    xs = []
    for i in range(r-1):
        xi = binomial_dlog_sub(y, g, p, q, i + 2)
        xs.append(xi)
        y = ZZ(y * pow(g,-xi,p^r) % p^r)
        g = ZZ(pow(g,p,p^r))
    return ZZ(xs, p)

x0 = 371400036118087873423099736623135345907801208559021371167756375819427925457040761043671101071645449151098283672036345482928921105303474546205199698226967922594539121528410724439325649997319457455755409700098207768114873790937028312
x1 = 407962438778688190907253749251184015390900029410795727241330663524055399813222240683911556296466108640007883599111746506669376054290340161271688994440216754019475823593004413780334836609175487467226663558545269470313125327004442075
y0 = 0
y1 = 94677558707295712242090997386462549942626176729545589690797827556684121785602596433846894851887708797985968631940880045924727539798391064801973678296817051938196633805006754526493164114864007544162629920939963968396975696320276490

a0 = binomial_dlog(y1, x1, p, p-1, 3)

Zp = GF(p)
Zp3 = Zmod(p^3)

p1 = 2^2 * 11 * 1399 * 576647 * 707717 * 31455197 * 99986015309131554073222673357191122700463502810799771
mul = 99986015309131554073222673357191122700463502810799771

Y = Zp(Zp3(y1)**(p^2))^mul
base = Zp(Zp3(x1)**(p^2))^mul

a1 = Y.log(base)
a = crt([int(a0), int(a1)], [p^2, base.multiplicative_order()])
mod = ZZ(p^2 *  base.multiplicative_order())
print(ZZ(a).nbits())
while M^a != Ma and a <= 2** 590:
    a += mod
print(M^a == Ma)

S = Mb^a
key = sha256(S.str().encode()).digest()
ct = AES.new(key, AES.MODE_ECB)
print(ct.decrypt(bytes.fromhex("b7df98ace3796355c2a3a9230760569b53814889e975fe2f50992b3e1683898d918ab7f392f80628b7a0dc3a43e854b7")))

其中 x0, x1, y0, y1 分布是矩阵 M,Ma 的特征值，即 f(x),g(x)在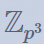上的两个根。可以在 sage 上先求 f(x),g(x) 在有限域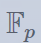上的根，再用 hensel lift 提升到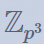上。这里我直接用 mathematica求解了：

(* Define the coefficients and modulus *)
p := 79008119711208495443423312926395331665944721527891616265679009115440018598629;
(* Define the polynomial f in Z/pZ *)
f[x] := x^8 + 4093721904954649749606358934675410877292635281608771685862726636369665899324049086150200562854544440601246934938901527213598536175425903260985087743234878654868746038343801085190715017197498882769768591199871359795327990234738452*x^7 + 367404874475222387519073916907607961923077180133950813993464335269572747847813029278054827018133545487170438196450169909581908989309791181552180719538770868379479610175045121045846011951922292965503309708454446782292865326354321912*x^6 + 177334381872630257189629062824772654460770746386380579458039259995516290683569877558372571466169688824767087952270911510631825690238016500401661685288325571920772075384649686856653423431074103598988709403801098205856723623333681089*x^5 + 25191499168181107412437851008691236552090785169335778784797321829257870553430277472174832165558853630912648697448537008692742793725787528623900341901945473720349046980767934257022002486292212825598159144175849009096073120750110708*x^4 + 396146105968377561971413800203188312165286560688315616565875611261869359828317850466464787734547459646930894335610514896816087180411289857829908664253281532555182805130150257075264952976931524355114878698659788787262594603835518672*x^3 + 381138907203975870155852768799735039151665548460274957357873912957626986007659000764914336251584929202433067073068146179092633270125307617583862079189344893760630090246984172008202072467706057674857651545098447363477781867327938364*x^2 + 161260580627308331569341352068126494754224600502498963925722554030645210124389434053266166051019415845959899110109398619984901663335528783735605538278492621074006336756950889394251274080252889880009127570263041624925038033523029421*x + 413764393906813184792095848510130371922881920023911304091412811929182653159775620076043917208494157146619150259903492673279265236497447469592287019273944349330530789050819605174812787757614659885026798291564621732946375926375006296;
g[x] := x^8 + 357903988503903976310732651031359779456379849522196653774615909583867474471617134302475726478216182145155130774807507683294704460917948858573155532471596800225612292578085080007681631917945693197958570787234880779035256523087088146*x^7 + 311636578648508530239910773146241316877102755967447686380563068290147162450253521576340879246066824085062939261435498362155810709871154439293375633684590378626012386323072575201423052458514067266623020807167337805350680795210821820*x^6 + 117015207887053032786663797141866564004058600362253644593264858884056606550611109995332728807188414704268152220580397456546906528851625435103021586071494073587676639916393933478813286647474108554658766482331742501554836405007837375*x^5 + 224342411932397217007619412289303423058762311626908283822307925570940590311213986659094339000758599105468045261488350030708622179712449074336442353775805174995452840694623971152908201182742816937866830213548088951630800788388434305*x^4 + 120930329003423380859670636895907754542373341576407870509476998443806299696140859040711832644377542687558553388824898864820174969990871338388950173774587014914485784415193477275448997602686307946551403726070084852772327563262527597*x^3 + 292404292222921897311799124254162395717600857119035716250294527741379227387404311920192136651670934332110659439794535284287560732288202548526736358648929391394032305758746184927511154299606281729777193145022853760459605761534879020*x^2 + 74454489175073809641153530871664457671827845767468333147461996707841855013367595906893910316935518792989091887399143758486348371790431082934982081896791848607332034660255575899354011412205783713075301952880726144940039361979930166*x + 393416694638142524750100170140458906208125208258700143703725549348274340236036132161116111232336035596971628675984584198222395607679769778561975324755324699674486626508048092414419036308362221567055058235620849947595976046717007123;
h[x] := x^8 + 368269120925204307841638327556948738248008244125731087147105096669170482412087584298762137907624773157798580984866033842606103477082252536842968503239061956145574790452327950261552851529507422848613945044288042613453545261800562362*x^7 + 449987731040989555283524165593813556898401269388580458721035665656162896969629741000855251321475075461109798893240439786954837572392778981054303607758928730006332187648539734391205404883529617372296489142105170402913366290591589740*x^6 + 315418547499633345392692344954180275019174677207144238359964877611104826486726937454748921493980865657816511973367329719661631627946866276458657425622819251228387377192666567121428717314596169496731742858824534979717357335840613607*x^5 + 357909544837229707057359443484388962909430770601278015707741754050659433117950318750953725540033131359803951561263608761005282602211766593615790673519145241570540678883082397165755590201315385600689712763058785708012630927021015442*x^4 + 246061747288761165012261995041917910935269117055506858418748004180811864382219533116850701514640182362058341780787561524646475327973898671496575181095377907905327250509728812525313338583849889563081405382561891702685518251045293274*x^3 + 430601056189771169060473697251681998594583340481523396377723692328240124694720819648643889047576099881196198137600199015062592272307653394226275979208399274531789071358322469832950513437823717746685529911962147299510394594413915175*x^2 + 234403107081945116834803895162301189269956100903518622544423778907405517401924750605427807243208280024444940995702993946139220601976517221891377752705109832132861241029489979063069092260272670419957488928327202997129512498577024243*x + 68949233104895068629161700695057239723772333765445437619294192398176878421690981871123893501268425231806444217667529637506709676576508980597776877826088053142809878710778128740433510685977745515942737195019639799393230028795807852;
ft[x] := x^8 + 383920099870381608102679618015482807080034657997477982984847489791362980720311960947351862170344930551152208389149649138480137028957261298482739170415206382617500078007029408290585464942078921851408987667043010665525967029978688463*x^7 + 394206684508048240243624297535915526066956374553945445983903555429057896585449749758395637144584707372879613230391062687618298449282731229616040337707834909712506476603365161874078410555211280633951945940401970857623218200671827883*x^6 + 312801951513663194322507779483868062445057002572750198980778949177011830144159407278276789689965006295366754231046802568030645268550994304076780844150544812512495802058735488405413107938517891583814469390245800499624339536286374855*x^5 + 304207453426368455507260187000259161680797949568419015777394807234726874491379008905558121156820132438483555233884493383223568543054633212003192558809097263287599578337744519127944876767224257734103877638998768798162729742751991334*x^4 + 488562390330112251478434104913270615058262148137982246783050632672662540547064271508604551022541383243304829441148248777045421518613585806618630339151672406292309796942570399832915255125641579770361241189535652893809636997439785322*x^3 + 144489347592968678787407504351401235198915423461420719116662121544104535471631682422539775209665816346826052055939971260908543461450841862957774694172584169701114788733704140536189258575554047116698068261490832372692955989354174512*x^2 + 124336184705752994134771898031783603840671691645039515066329721578664551092115390224225361135813467825526051625152503952305596009438928297445789596850098467564702395014816196405236987961824640971073471825540280490658060513628382584*x + 336520107435644163849838386892958313265970888242623423350900283498518657722601397840454302187254724581953043560858119852844556859641614596148559146300448856496199110834310343477209142710586778061610864993369700792617629390271865950;


(* Find the roots of f in Z/pZ *)
froots = Roots[f[x] == 0, x, Modulus -> p^3];
groots = Roots[g[x] == 0, x, Modulus -> p^3];
hroots = Roots[h[x] == 0, x, Modulus -> p^3];
ftroots = Roots[ft[x] == 0, x, Modulus -> p^3];

For [i = 1, i <= Length[froots], i++,
  Print["Solution of f(x): ", froots[[i, 2]]];
]

For [i = 1, i <= Length[groots], i++,
  Print["Solution of g(x): ", groots[[i, 2]]];
]

For [i = 1, i <= Length[hroots], i++,
  Print["Solution of h(x): ", hroots[[i, 2]]];
]

For [i = 1, i <= Length[ftroots], i++,
  Print["Solution of ft(x): ", ftroots[[i, 2]]];
]

RSA

调整dbits = 0x240，使得原本easyRSA的脚本无论如何调整t的大小都无法获得结果。

同样的等式

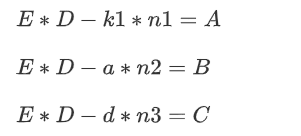
各个数的大小有

复现的时候对于卡了t的界的问题自己提了个比较粗浅地推导==：

对于easyRSA里的这个格，同样利用高斯启发式考虑。

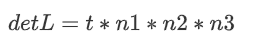
期望最短向量长度为

转换为比特位即：

但此时再次计算目标向量中的D*t，可以发现其位数为

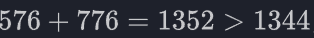
即此时目标向量长度改变，tbit不再能满足需求，也就推出矛盾了

时间线稍后，队友复盘提到了格攻击之小未知数方程求解入门——原理与例子 | Tover’ Blog，里面提到了配平技巧。

文章的大致意思指，一般情况下先配平，再去考虑高斯启发式，否则格可能会无法满足需求，配平即使目标向量中各个数的大小平衡。

对于midRSA这个题而言，就是令tbit=768，有|w|=1344

此时可求得α(L)=1342.5<1344不满足要求，这样就可以看到所谓的卡界了。

总而言之，以上是对于卡界的解释，接下来是解题部分。

解法一：

通过爆破部分位并构造新格来解决问题。

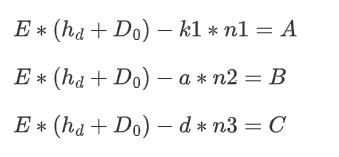
当我们爆破hd时，构造

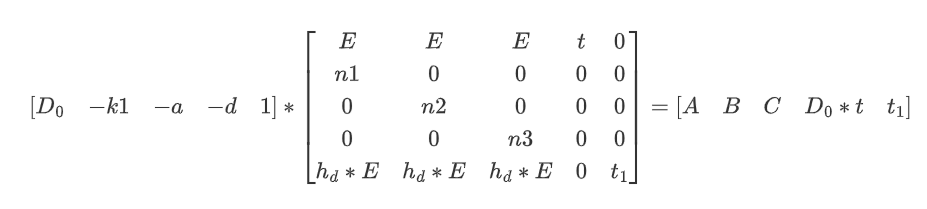
这里重新推导，在令的部分应

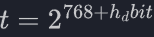
此时重新计算

得为满足需求应有

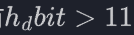
因为算的比较粗略，hd bit需求可能要更大才能爆破出来，比如一起复现的队友算出来要爆破16位。

实测结果是10位

然后爆高位和低位没有影响，无非爆高位可以少爆一位

这里贴个爆高位的脚本：

from Crypto.Util.number import long_to_bytes
from tqdm import tqdm
c = 598823083137858565473505718525815255620672892612784824187302545127574115000325539999824374357957135208478070797113625659118825530731575573239221853507638809719397849963861367352055486212696958923800593172417262351719477530809870735637329898331854130533160020420263724619225174940214193740379571953951059401685115164634005411478583529751890781498407518739069969017597521632392997743956791839564573371955246955738575593780508817401390102856295102225132502636316844
e = 334726528702628887205076146544909357751287869200972341824248480332256143541098971600873722567713812425364296038771650383962046800505086167635487091757206238206029361844181642521606953049529231154613145553220809927001722518303114599682529196697410089598230645579658906203453435640824934159645602447676974027474924465177723434855318446073578465621382859962701578350462059764095163424218813852195709023435581237538699769359084386399099644884006684995755938605201771
n1 = 621786427956510577894657745225233425730501124908354697121702414978035232119311662357181409283130180887720760732555757426221953950475736078765267856308595870951635246720750862259255389006679454647170476427262240270915881126875224574474706572728931213060252787326765271752969318854360970801540289807965575654629288558728966771231501959974533484678236051025940684114262451777094234017210230731492336480895879764397821363102224085859281971513276968559080593778873231
n2 = 335133378611627373902246132362791381335635839627660359611198202073307340179794138179041524058800936207811546752188713855950891460382258433727589232119735602364790267515558352318957355100518427499530387075144776790492766973547088838586041648900788325902589777445641895775357091753360428198189998860317775077739054298868885308909495601041757108114540069950359802851809227248145281594107487276003206931533768902437356652676341735882783415106786497390475670647453821
n3 = 220290953009399899705676642623181513318918775662713704923101352853965768389363281894663344270979715555659079125651553079702318700200824118622766698792556506368153467944348604006011828780474050012010677204862020009069971864222175380878120025727369117819196954091417740367068284457817961773989542151049465711430065838517386380261817772422927774945414543880659243592749932727798690742051285364898081188510009069286094647222933710799481899960520270189522155672272451
dbit=9
tbit=1344-576+dbit+1
for Dh in tqdm(range(2^dbit)):
    Dh = int('1' + bin(Dh)[2:].zfill(dbit), 2) << (576-dbit-1)
    M = Matrix(ZZ,[[e, e, e, 2^tbit, 0],
                [n1, 0, 0, 0, 0],
                [0, n2, 0, 0, 0],
                [0, 0, n3, 0, 0],
                [e*Dh, e*Dh, e*Dh, 0, 2^1344]
                ])
    res = M.LLL()
    for i in res:
        if abs(i[-1])==2^1344:
            d = int(i[3]//2^tbit) + Dh
            flag = long_to_bytes(int(pow(c,d,n1)))
            if b'ACTF{' in flag:
                print(flag)
                break

解法二：

在解法一的错误计算中产生的想法（虽然不知道原博主是不是这样）

总之，为减小|w|，进而想到爆破ABC的部分位.

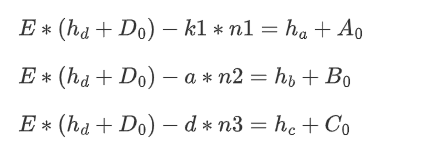
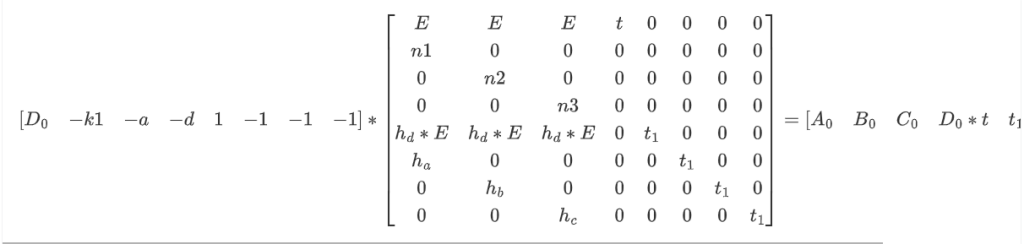
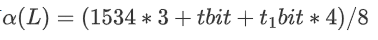
FORENSICS

卫继龚的电脑1

Passware Kit Forensic 选择内存镜像分析，勾选Windows用户进行分析

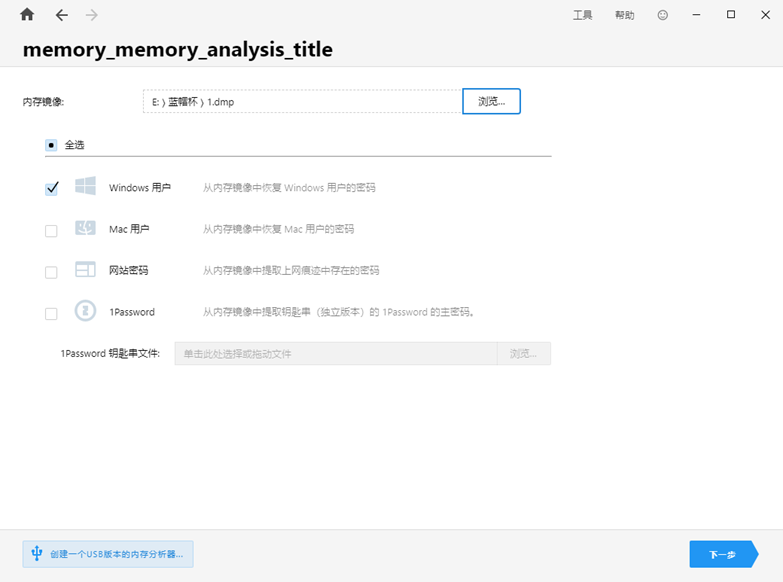
获取密码为anxinqi

卫继龚的电脑2

取证大师内存工具分析，发现MagnetRAMCapture这个进程，这个软件是专门用来制作内存镜像的工具

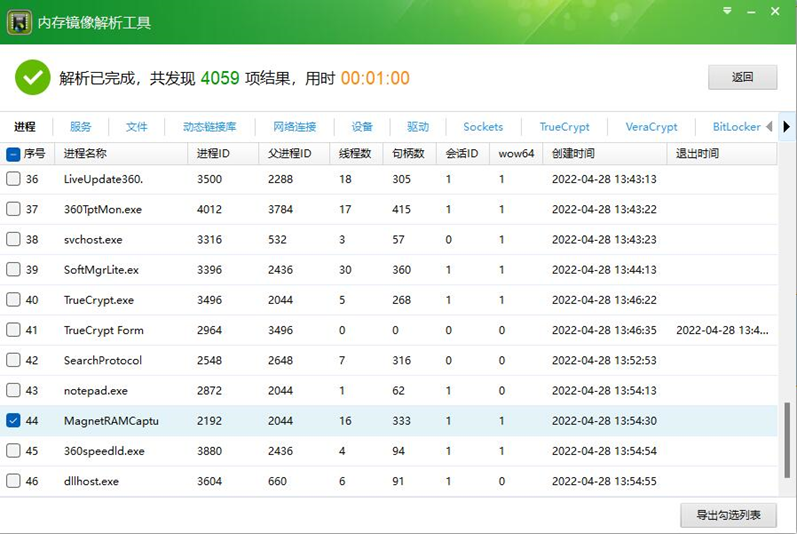
得到结果为2192

卫继龚的电脑3

Passware Kit Forensic 选择内存镜像和加密卷进行解密

获得未解密版镜像

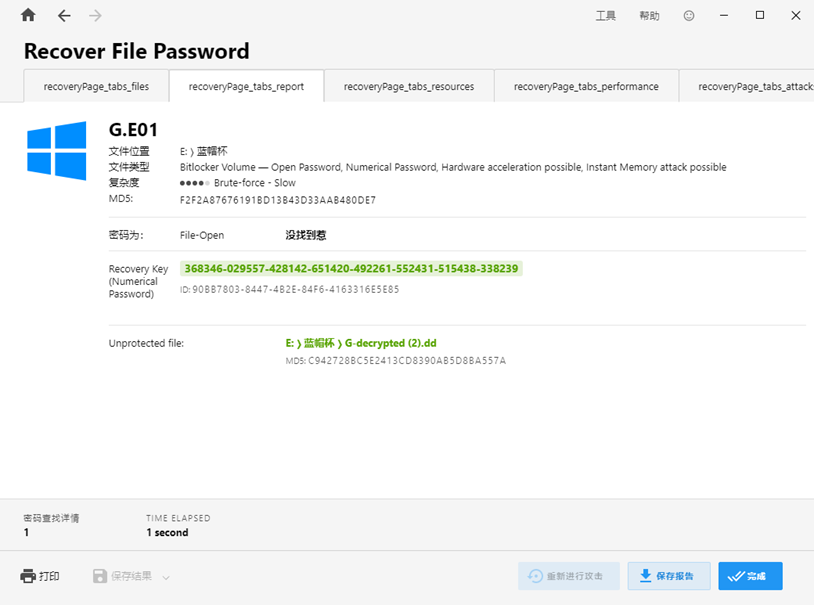
查看磁盘信息，发现多个office文件均被加密，还有一个pass.txt，推测需要跑字典

导出pptx docx pass.txt

Passware Kit Forensic添加pass.txt字典

跑密码

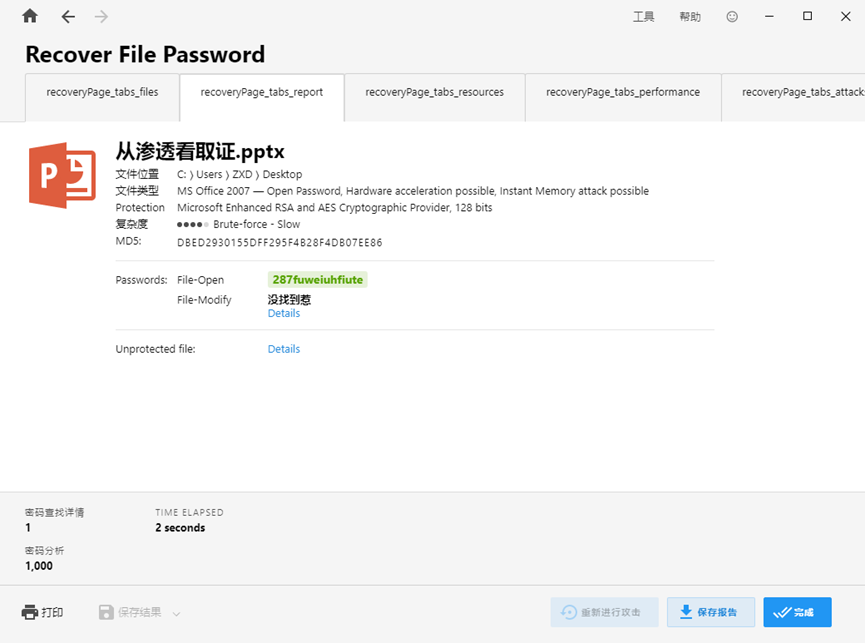
打开ppt输入密码

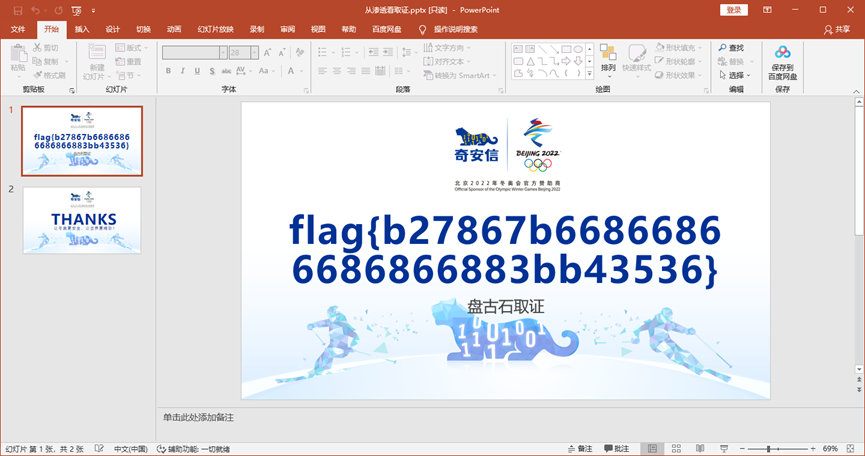
卫继龚的电脑4

导出未加密镜像中的新建文本文档.txt

Passware Kit Forensic中添加内存镜像和新建文本文档.txt获得解密后的镜像

Ftk imager打开查看，找到一个压缩包

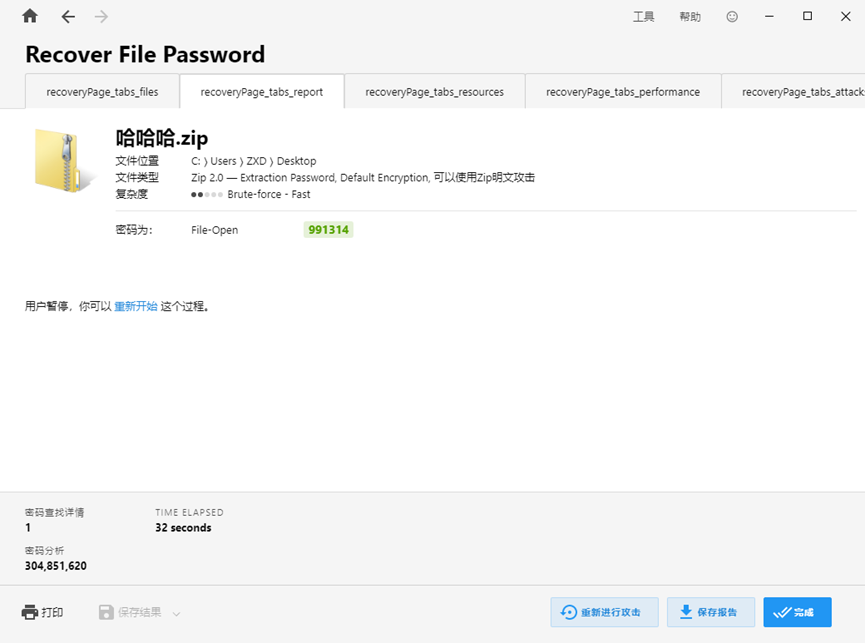
导出哈哈哈.zip 用Passware Kit Forensic爆破压缩密码

得到密码为991314

解压zip中的txt

秘密

附件是一个vhd，所以我们只要知道主密钥，私钥，以及用户登录密码即可，利用advanced efs data recovery

先把vhd挂载到本机，只会扫描key得到主密钥和私钥，之后就是找用户密码即可

后来发现可以爆破，直接利用rockyou字典爆破即可

查看即可得到密码为

superman

BLOCKCHAIN

托尼的合同

题目给了一个公网上的合约https://testnet.ton.cx/address/EQAM2HjRB-PFaD2mlJ5QjQAlfRAcmZ-j9ydT_54FzmbffN6E，换一个区块浏览器是 https://testnet.tonscan.org/address/EQAM2HjRB-PFaD2mlJ5QjQAlfRAcmZ-j9ydT_54FzmbffN6E。因为是公网，所以应该就不是需要发交易的，有合约字节码，所以先考虑逆向合约。

题目合约反汇编:

SETCP0
(:methods
recv_internal: 
    2 2 BLKDROP2
    c4 PUSH
    CTOS
    8 LDU
    s1 POP
    32 LDU
    s0 s2 XCHG
    32 PUSHINT
    SDSKIPFIRST
    NOW
    ROT
    LESS
    6 THROWIF
    s0 PUSH
    SBITS
    344 PUSHINT
    EQUAL
    6 THROWIFNOT
    PUSHNULL
    s2 PUSH
    SEMPTY
    NOT
    <{
    s0 POP
    s0 s1 XCHG
    LDDICT
    ROTREV
    }> PUSHCONT
    IF
    s0 s3 XCHG
    CTOS
    4 PUSHINT
    SDSKIPFIRST
    LDMSGADDR
    s0 POP
    s0 s1 XCHG
    48 LDU
    s0 s1 XCHG
    92703703713403 PUSHINT
    EQUAL
    6 THROWIFNOT
    NIL
    11000385076366155543686602566826962197403024283852028545596640486225 PUSHINT
    SETRAND
    36 PUSHINT
    PUSHREFCONT
    REPEAT
    s4 POP
    8 LDU
    s0 POP
    125 EQINT
    6 THROWIFNOT
    35 PUSHINT
    s0 PUSH
    PUSHREFCONT
    REPEAT
    s0 POP
    0 PUSHINT
    36 PUSHINT
    PUSHREFCONT
    REPEAT
    s1 s3 XCHG
    s0 s1 XCHG
    8 LDU
    233 PUSHINT
    ROT
    MUL
    8 PUSHPOW2
    RAND
    ADD
    8 PUSHPOW2DEC
    AND
    8 PUSHPOW2
    RAND
    XOR
    s5 PUSH
    -8 PUSHINT
    DICTUGET
    NULLSWAPIFNOT
    s0 POP
    8 LDU
    s0 POP
    s1 s2 XCHG
    TPUSH

recv_external: 
    s0 POP
    c4 PUSH
    CTOS
    8 LDU
    s0 s1 XCHG
    0 EQINT
    6 THROWIFNOT
    ACCEPT
    32 LDU
    PUSHNULL
    s1 PUSH
    SEMPTY
    NOT
    <{
    s0 POP
    LDDICT
    s0 s1 XCHG
    }> PUSHCONT
    IF
    s0 s1 XCHG
    288 PUSHINT
    LDSLICEX
    s0 POP
    1 PUSHINT
    NEWC
    8 STU
    s1 s3 XCHG
    32 STU
    STDICT
    s0 s1 XCHG
    STSLICER
    ENDC
    c4 POP
) 19 DICTPUSHCONST
DICTIGETJMPZ
11 THROWARG

首先简单学一下这个链，一些材料：

得到了以下信息：

TON 中的账户不区分 ETH 一样的 EOA 和合约账户，一切皆合约
合约地址是 32 字节数，同时有包装了校验信息等再 base64 的 user-friendly 地址写法
- https://docs.ton.org/learn/overviews/addresses
合约采用 FunC（高级）或 Fift（低级）语言编写，编译到 TVM 字节码
合约部署的时候有 code 和 data 两个部分
- 都是存在链上的，code 部分是合约的字节码，data 部分是合约的数据（可修改）
- 部署方式应该类似 ETH 是通过执行 deploy bytecode 来同时部署 code 和 data（没细看）
code、data、message 等的表示方式都是使用 bag of cells (boc) 来编码的
- https://docs.ton.org/develop/data-formats/cell-boc
- cell 是 TON 中的一个基本结构，可以存储 1023 个 bit，并且带有最多四个指向其他 cells 的reference
- cell 的编码有点复杂，可以看链接里的示例
- cell 逐个链接形成的整体就是 bag of cells，编码就是将所有 cell 打包
- 区块浏览器解析出来的 cells 结构就是 boc 的树形结构
  - 缩进代表 ref 的子节点，x{} 中的内容就是 cell 的内容
  - x{} 中带有的下划线表示将最后一个 1 以及后面所有的 0 删掉（以此表示非 8 的倍数的 bit）
- message 等的规范文档里通过引入了一个新的叫 TL-B 的语言来规定（看起来好复杂好蠢）
  - https://docs.ton.org/develop/data-formats/msg-tlb
TVM 是一个栈式虚拟机，指令很多（类似 CISC），有一个临时的栈和一些寄存器
- https://docs.ton.org/learn/tvm-instructions/tvm-overview
- 栈上元素可以有类型：
  - 257bit 整型、元组、Null
  - cell、slice（可读的 cell）、builder（可写的 cell）、continuation（一组可执行的字节码）
- 栈的初始化依次 push balance value raw_message message_body funcion_selector（internal 调用的情况）
  - https://docs.ton.org/learn/tvm-instructions/tvm-initialization#internal-message
- 寄存器 s0 就表示栈顶元素，s1 表示栈顶第二个元素，以此类推
  - 其实就是别名，不是独立于栈之外的寄存器
- 有 c0-c7 八个控制寄存器：
  - 其中比较重要的有 c4 初始表示合约的 data 部分，c7 初始表示一些临时数据
  - https://docs.ton.org/learn/tvm-instructions/tvm-overview#control-registers
- 默认有两个函数，链上合约之间调用会触发 recv_internal，从外部调用会触发 recv_external
- 调用的时候先初始化栈和寄存器，然后执行字节码
  - 字节码开头一般会读取 function_selector 判断调用的函数，然后跳转到对应的代码段（0 表示 internal，-1 表示 external）
  - 这时候可以从栈上读取 message 内容，从 c4 中读取 data 部分内容
- 具体的指令可以看文档，或者文档源码 GitHub 里的 csv 表格
  - https://docs.ton.org/learn/tvm-instructions/instructions

接下来是题目，对着字节码模拟栈逆了 external 发现其实什么都没干，所以其实主要逻辑都在 internal中。字节码里出现了 LDDICT 指令，即从栈顶的 cell 中提取出一个 dict，但 dict 是什么、怎么解析都不太清楚，所以干脆找动调的手段了。

可以搜到 ton-community/ton-contract-executor，可以在本地不需要 TON 网络就执行一个合约，需要 yarn 装一下依赖，然后编写一个 main.mjs:

import { SmartContract, internal, externalIn } from "ton-contract-executor";
import { Cell, BitString } from "@ton/core";

async function main() {
    let contract = await SmartContract.fromCell(
        Cell.fromBoc(Buffer.from("...", "hex"))[0],
        Cell.fromBoc(Buffer.from("...", "base64"))[0],
        {debug: true}
    );
    const msgBody = new Cell();
    console.log(msgBody);
    const res = await contract.sendInternalMessage(
        internal({
            dest: contract.address,
            value: 0n,
            bounce: false,
            body: msgBody,
        })
    )
    console.log(res);
    console.log(res.logs);
}

await main();

这样给合约开启 debug 之后就可以输出每次执行指令的信息，以此可以解决不知道挂在哪里以及PUSHREFCONT 在网站上没有具体反汇编的问题。

接下来知道了运行时挂在了开头，因为开头读取的 data[1:5] 作为 timestamp 和当前的时间比较，如果在data 设定的以前就 throw 6 异常，所以干脆在代码里把 LESS(B9) 改为 GEQ(BE) 就可以了。接下来后面的部分就可以正常执行了，根据每条指令来模拟栈，得到以下的栈变化分析：

msg_raw message data
msg_raw message data[8:]
msg_raw message data[8:40] data[40:]
msg_raw data[40:] data[8:40] message
msg_raw data[40:] data[8:40] message 32
msg_raw data[40:] data[8:40] message[32:] now
msg_raw data[40:] message[32:] now data[8:40]
msg_raw data[40:] message[32:] -1
msg_raw data[40:] message[32:]
msg_raw data[40:] message[32:] message[32:]
msg_raw data[40:] message[32:] 344
msg_raw data[40:] message[32:] 344 344
msg_raw data[40:] message[32:] 0
msg_raw data[40:] message[32:] null
msg_raw data[40:] message[32:] null 1
msg_raw data[40:] message[32:] null 1 cont1
    msg_raw data[40:] message[:32] null
    msg_raw data[40:] message[:32]
    msg_raw message[32:] data[40:]
    msg_raw message[32:] D data[40+dict:]
    msg_raw data[40+dict:] message[32:] D
D data[40+dict:] message[32:] msg_raw
D data[40+dict:] message[32:] msg_raw 4
D data[40+dict:] message[32:] msg_raw[4:]
D data[40+dict:] message[32:] msg_raw.src msg_raw[src:]
D data[40+dict:] message[32:] msg_raw.src
D data[40+dict:] msg_raw.src message[32:]
D data[40+dict:] msg_raw.src message[32:32+48] message[32+48:]
D data[40+dict:] msg_raw.src message[32+48:] message[32:32+48]
D data[40+dict:] msg_raw.src message[32+48:] message[32:32+48] 92703703713403
D data[40+dict:] msg_raw.src message[32+48:]
D data[40+dict:] msg_raw.src message[32+48:] ()
D data[40+dict:] msg_raw.src message[32+48:] () 11000385076366155543686602566826962197403024283852028545596640486225
D data[40+dict:] msg_raw.src message[32+48:] ()
D data[40+dict:] msg_raw.src message[32+48:] () 36
D data[40+dict:] msg_raw.src message[32+48:] () 36 refcont
    D data[40+dict:] msg_raw.src message[32+48:] ()
    D data[40+dict:] msg_raw.src () message[32+48:]
    D data[40+dict:] msg_raw.src () message[32+48:32+56] message[32+56:]
    D data[40+dict:] msg_raw.src () message[32+48:32+56] message[32+56:] 233
    D data[40+dict:] msg_raw.src () message[32+56:] 233 message[32+48:32+56]
    D data[40+dict:] msg_raw.src () message[32+56:] 233*message[32+48:32+56]
    D data[40+dict:] msg_raw.src () message[32+56:] 233*message[32+48:32+56] 256
    D data[40+dict:] msg_raw.src () message[32+56:] 233*message[32+48:32+56] rand(256)
    D data[40+dict:] msg_raw.src () message[32+56:] 233*message[32+48:32+56]+rand(256)
    D data[40+dict:] msg_raw.src () message[32+56:] 233*message[32+48:32+56]+rand(256) 255
    D data[40+dict:] msg_raw.src () message[32+56:] (233*message[32+48:32+56]+rand(256))&(255)
    D data[40+dict:] msg_raw.src () message[32+56:] (233*message[32+48:32+56]+rand(256))&(255) rand(256)
    D data[40+dict:] msg_raw.src () message[32+56:] ((233*message[32+48:32+56]+rand(256))&255)^rand(256)
    D data[40+dict:] msg_raw.src () message[32+56:] ((233*message[32+48:32+56]+rand(256))&255)^rand(256) D
    D data[40+dict:] msg_raw.src () message[32+56:] ((233*message[32+48:32+56]+rand(256))&255)^rand(256) D 8
    D data[40+dict:] msg_raw.src () message[32+56:] D[((233*message[32+48:32+56]+rand(256))&255)^rand(256)] ?
    D data[40+dict:] msg_raw.src () message[32+56:] D[((233*message[32+48:32+56]+rand(256))&255)^rand(256)][:8] D[((233*message[32+48:32+56]+rand(256))&255)^rand(256)][8:]
    D data[40+dict:] msg_raw.src () message[32+56:] D[((233*message[32+48:32+56]+rand(256))&255)^rand(256)][:8]
    D data[40+dict:] msg_raw.src message[32+56:] () D[((233*message[32+48:32+56]+rand(256))&255)^rand(256)][:8]
    D data[40+dict:] msg_raw.src message[32+56:] (D[((233*message[32+48:32+56]+rand(256))&255)^rand(256)][:8])
... exec refcont for 36 times ...

D data[40+dict:] msg_raw.src message[...:] flag_content
flag_content data[40+dict:] msg_raw.src message[...:]
...
flag_content data[40+dict:] msg_raw.src 35
flag_content data[40+dict:] msg_raw.src 35 35
flag_content data[40+dict:] msg_raw.src 35 35 refcont
    flag_content data[40+dict:] msg_raw.src 35
    flag_content data[40+dict:] msg_raw.src 35 35
    flag_content data[40+dict:] msg_raw.src 35 36
    flag_content data[40+dict:] msg_raw.src 35 rand(36)
    flag_content data[40+dict:] msg_raw.src 35 rand(36) flag_content 35
    flag_content data[40+dict:] msg_raw.src 35 rand(36) flag_content[35]
    flag_content data[40+dict:] msg_raw.src 35 rand(36) flag_content[35] (flag_content) rand(36)
    flag_content data[40+dict:] msg_raw.src 35 rand(36) flag_content[35] flag_content[rand(36)]
    flag_content[35] data[40+dict:] msg_raw.src 35 rand(36) flag_content flag_content[rand(36)] 35
    flag_content[35] data[40+dict:] msg_raw.src 35 rand(36) flag_content{35=flag_content[rand(36)]}
    35 data[40+dict:] msg_raw.src flag_content{35=flag_content[rand(36)]} flag_content[35] rand(36)
    35 data[40+dict:] msg_raw.src flag_content{35=flag_content[rand(36)], rand(36)=flag_content[35]}
    flag_content{35=flag_content[rand(36)], rand(36)=flag_content[35]} data[40+dict:] msg_raw.src 35
    flag_content{35=flag_content[rand(36)], rand(36)=flag_content[35]} data[40+dict:] msg_raw.src 34

    flag_content_modified data[40+dict:] msg_raw.src 34
    flag_content_modified data[40+dict:] msg_raw.src 34 34
    flag_content_modified data[40+dict:] msg_raw.src 34 35
    flag_content_modified data[40+dict:] msg_raw.src 34 rand(35)
    flag_content_modified data[40+dict:] msg_raw.src 34 rand(35) flag_content_modified 34
    ...

    flag_content_modified data[40+dict:] msg_raw.src 0
flag_content_modified data[40+dict:] msg_raw.src
flag_content_modified data[40+dict:] msg_raw.src 0
flag_content_modified data[40+dict:] msg_raw.src 0 36
flag_content_modified data[40+dict:] msg_raw.src 0 36 refcont
    flag_content_modified data[40+dict:] msg_raw.src 0
    flag_content_modified data[40+dict:] msg_raw.src 0 flag_content_modified 0
    flag_content_modified data[40+dict:] msg_raw.src 0 flag_content_modified[0]
    flag_content_modified flag_content_modified[0] msg_raw.src 0 data[40+dict:]
    flag_content_modified flag_content_modified[0] msg_raw.src 0 data[40+dict:48+dict] data[48+dict:]
    flag_content_modified data[48+dict:] msg_raw.src 0 flag_content_modified[0] data[40+dict:48+dict]
    flag_content_modified[0]==data[40+dict:48+dict]?

这样看整体的逻辑就是：

input = input[4:]
if input[:6] != "TPCTF{":
    throw 6
flag = []
setrand(11000385076366155543686602566826962197403024283852028545596640486225)
for i in range(36):
    flag.append(D[((233*input[i]+rand(256))&255)^rand(256)][0])
for i in range(35, 0, -1):
    a = rand(i + 1)
    flag[i], flag[a] = flag[a], flag[i]
for i in range(36):
    if flag[i] != data_after_dict[i]:
        throw 666

为了拿到其中的数据需要让 executor 在运行中输出栈的内容，通过阅读代码知道 ton-contract-executor 最终调用了 ton 官方 vm-exec 分支里编译好的 wasm 来跑指令，同时也给了 builder ton-community/ton-vm-exec-builder（这个 builder 的 README 有问题，clone ton 源码的时候需要加 –recursive），所以就可以 patch ton 的源码重新编译生成 wasm 载入 executor 了。在 ton-blockchain/crypto/vm/vm.cpp 中 VmState::step() 开头的地方加入栈的输出代码：[](https://note.tonycrane.cc/writeups/tpctf2023/#__codelineno-4-1)std::ostringstream os; [](https://note.tonycrane.cc/writeups/tpctf2023/#__codelineno-4-2)stack->dump(os, 3); [](https://note.tonycrane.cc/writeups/tpctf2023/#__codelineno-4-3)VM_LOG(this) << "stack:" << std::move(os).str();

这样就可以拿到其中出现的所有值了，不过最后的判断只要有不一样的就会抛出 666 结束执行而不显示后面的data_after_dict 值，所以为了 dump 出这部分还需要 patch 一下 contops.cpp 里exec_throw_fixed，使得 excno 为 666 时 return 0。之后得到所有栈输出，根据正则 (\d+?) (\d+?) CS 可以筛选得到 data_after_dict 的内容，根据正则 execute RAND.*?(\d+?) (\d+?) \] 可以筛选得到每次交换的 i 和 a，然后反过来交换回去得到第一个循环后的 flag：[](https://note.tonycrane.cc/writeups/tpctf2023/#__codelineno-5-1)[46, 254, 159, 162, 180, 48, 104, 193, 90, 2, 82, 236, 188, 10, 224, 196, 138, 170, 62, 151, 172, 27, 4, 209, 58, 16, 27, 88, 32, 46, 161, 174, 86, 193, 135, 101]

第一个循环里的运算比较复杂而且有截断，还有 D 字典的结构也不太了解。因为每一位的计算和其他位都没有关系，所以选择从前往后的方法，逐位爆破 flag：

import os
import re
from tqdm import trange

target = [46, 254, 159, 162, 180, 48, 104, 193, 90, 2, 82, 236, 188, 10, 224, 196, 138, 170, 62, 151, 172, 27, 4, 209, 58, 16, 27, 88, 32, 46, 161, 174, 86, 193, 135, 101]
template = "4141414154504354467b%s7d"

flag = [0x41] * 36
for i in range(36):
    for j in trange(32, 127):
        flag[i] = j
        # logs = os.popen("node debug.mjs %02x" % j).read() # 65536 长度限制
        os.system("node debug.mjs %s > tmp" % (template % bytes(flag).hex()))
        with open('tmp', 'r') as f:
            logs = f.read()
        res = re.findall(r"..376; refs: 0..0\} (\d+?) CS\{Cell\{000", logs)
        if int(res[i]) == target[i]:
            print(bytes(flag))
            break

import { SmartContract, internal, externalIn } from "ton-contract-executor";
import { Cell, BitString } from "@ton/core";

async function main() {
    let contract = await SmartContract.fromCell(
        Cell.fromBoc(Buffer.from("te6cckECCAEAATgAART/APSkE/S88sgLAQIBIAIDBPjSbCLtRNDTBzHTHwKAINch+CNYufJGINdJgQFYuvKGbSLHALOVMAH0BFneA9B01yH6QDAB0y8BgiBUUENURnu68oZvAILQaHR0cHM6Ly95b3V0dS5iZS9kUXc0dzlXZ1hjUfgUgCSK5DTTBzDAffKGgCMgiuQwcIAkiuQTBAUGBwBi8jDtRNDTBwHAAPKG+ADTH20hxwCzlDD0BAHeAYEBINcYMHHIywcTyx/0AAHPFsntVABEAdMHgQDpWKiDB/gRoIQHsIMH+BGyJXj0Dm+hMNMHMBJvjAAuIKT4EVNBb4FTUW+BVBYDb4VAVW+FA6UAHFMwb4ED0wdQRLry4pqkAERfA3AggBjIywVQA88WgQKa+gISy2rLH4szY2NozxbJc/sAUXUrEg==", "base64"))[0], // patched
        Cell.fromBoc(Buffer.from("...", "hex"))[0], // not changed
        {debug: true}
    );
    let bf_content = process.argv[2];
    const msgBody = new Cell({bits: new BitString(Buffer.from(bf_content, "hex"), 0, 47 * 8)});
    const res = await contract.sendInternalMessage(
        internal({
            dest: contract.address,
            value: 0n,
            bounce: false,
            body: msgBody,
        })
    );
    console.log(res.logs);
}

await main();
process.exit();

这样爆破出来就能得到一个 uuid 就是 flag。

MISC#

卫继龚的日常#

Project-X#

RAW标志#

svg#

CRYPTO#

rlwe#

SPN#

MDH#

RSA#

解法一：#

解法二：#

FORENSICS#

卫继龚的电脑1#

卫继龚的电脑2#

卫继龚的电脑3#

卫继龚的电脑4#

秘密#

BLOCKCHAIN#

托尼的合同#